Activation

Posted on

对比、介绍神经元的激活函数。

img

Sgn

sgn(x)=0 if x<0 else 1sgn(x)=0\text{ if } x < 0 \text{ else }1

阶跃函数，sign

优点：理想的激活函数

缺点：不连续，x=0x=0 无导数，不好优化

Sigmoid

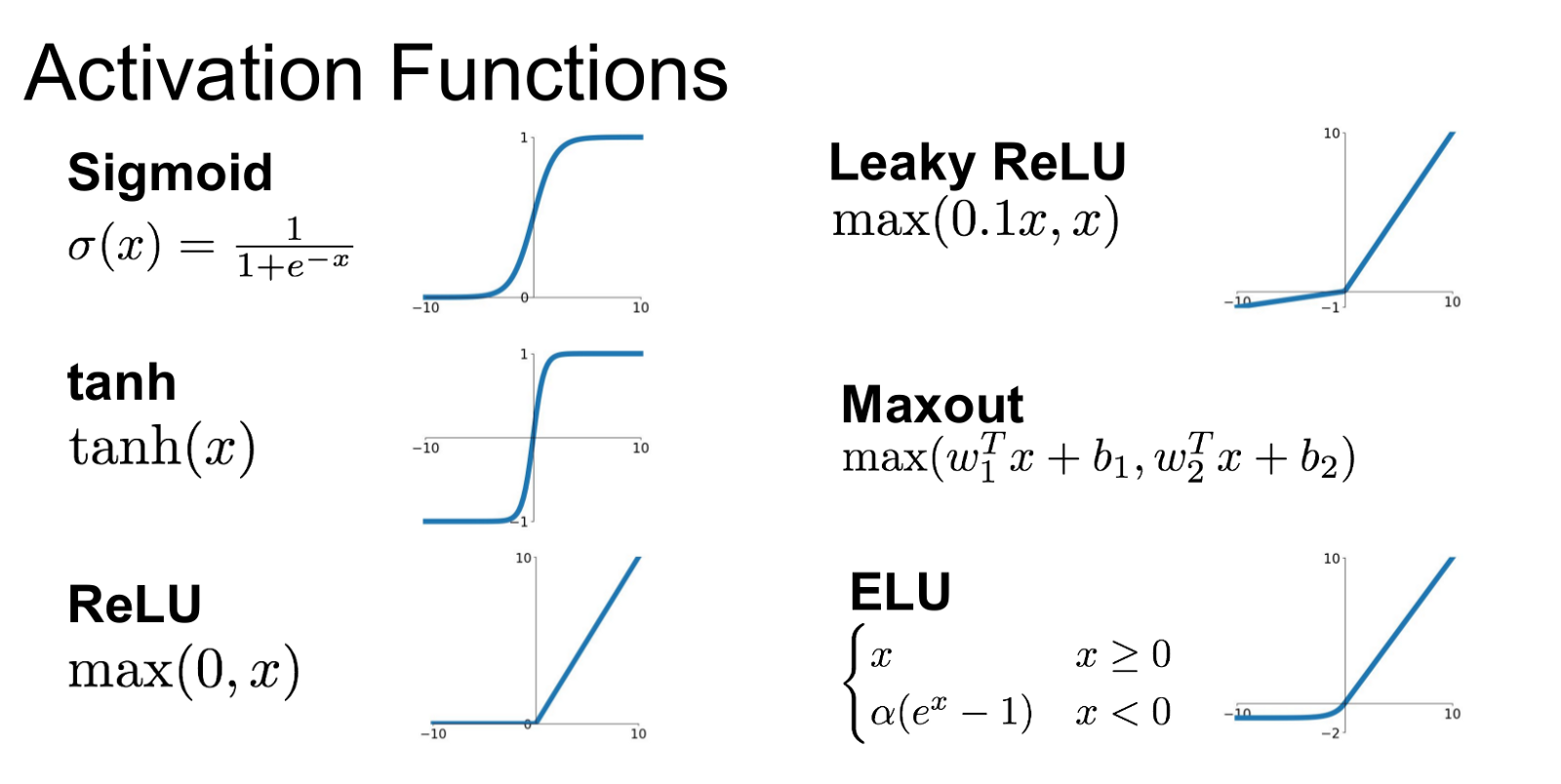
σ(x)=11+ex∈[0,1]σ′(x)=σ(x)(1−σ(x))\begin{aligned} \sigma(x)&=\frac{1}{1+e^x} \in [0, 1] \\ \sigma'(x)&=\sigma(x)(1-\sigma(x)) \end{aligned}

优点：

  • 函数与导数形式一致
  • 平滑连续可导，导数大于 0

缺点

  • 两端饱和，梯度弥散（当 ∣x∣>5|x|>5 时，梯度非常小，梯度更新缓慢）
  • exp 计算复杂度稍高，收敛慢
  • not zero-center 导致梯度从不同的方向更新？

Tanh

Hyperbolic tangent function [LeCun et al. 1991]

tanh(x)=2⋅σ(2x)−1∈[−1,1]tanh′(x)=1−(tanh(x))2\begin{aligned} \tanh(x) &=2 \cdot \sigma (2x) - 1 \in [-1, 1]\\ \tanh'(x) &= 1 - (\tanh (x))^2 \\ \end{aligned}

优点：

  • 在 x=0x=0 处梯度比 Sigmoid 更大
  • zero centered

缺点

  • 梯度弥散，当 saturated 时

ReLU

Krizhevsky et al. 2012 [7]

f(x)=max(0,x)∈[0,+∞]f(x)=max(0, x) \in [0, +\infty]

优点：

  • 最广泛使用，效果、性能权衡较好
  • 可以使系数稀疏 (x≤0x \leq 0)
  • 不饱和，避免梯度消失 (x>>0x >> 0)
  • 梯度简单，计算更快
  • 收敛较 sigmoid 更快

缺点

  • not zero center
  • 当 x<0x<0 时，有梯度弥散问题
  • 死亡神经元，Leaky ReLU 解决
  • 容易过拟合，用 droput 解决

Leaky ReLU

[Mass et al., 2013], [He et al., 2015]

f(x)=x if x>0 else axf(x)=x \text{ if } x \gt 0 \text{ else } ax

aa 是常数，一般 a=0.001a= 0.001

优点

  • 在 x<0x<0 时确保梯度存在，可以避免 ReLU 的 x<0x<0 的死亡神经元
  • 计算快
  • 比 sigmoid / tanh 收敛快（6x）

PReLU

f(xi)=x if x>0 else aix,ai≤1f(x_i)=x \text{ if } x \gt 0 \text{ else } a_ix, a_i \leq 1

其中 a 是可学习的参数。

Parametric ReLU [He et al., 2015] 提出，ImageNet 2014 超越人类的准确率。

ELU

[Exponetial Linear Units, Clever et al., 2015]

f(x)={xif x>0α(exp(x)−1)otherwisef(x)=\begin{cases} x &\text{if } x \gt 0 \\ \alpha (\exp (x) - 1) &\text{otherwise} \end{cases}

Maxout

由 Ian J. Goodfellow 等人在 ICML 2013 提出 [4]

max(w1Tx+b1,w2Tx+b2)\max (w_1^T x + b_1, w_2^T x + b_2)

优点

  • Generalize ReLU and Leaky ReLU
  • Linear Regime! 不饱和，不会死

缺点

  • 多一倍参数

Noisy ReLU

f(x)=max(0,x+Y),Y∼N(μ,σ2)f(x)=max(0, x+Y),Y \sim \mathcal{N} (\mu, \sigma^2)

Noisy ReLUs have been used with some success in restricted Boltzmann machines for computer vision tasks. [3]

TLDR

CSS231 Lecture 5 的实践建议

  • 用 ReLU，注意学习率
  • 可以试试 Leaky ReLU / Maxout / ELU
  • 可以试试 tanh 但不要期望太高
  • 不要用 sigmoid

Reference

[1] http://ufldl.stanford.edu/wiki/index.php/神经网络

[2] https://en.wikipedia.org/wiki/Rectifier_(neural_networks)

[3] Vinod Nair and Geoffrey Hinton (2010). Rectified linear units improve restricted Boltzmann machines. ICML. PDF

[4]He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2015). “Delving Deep into Rectifiers: Surpassing Human-Level Performance on Image Net Classification”. PDF

[5] Goodfellow I J, Warde-Farley D, Mirza M, et al. Maxout networks[J]. arXiv preprint arXiv:1302.4389, 2013. PDF

[6] CS231n Winter 2016 Lecture 5 Neural Networks VIDEO PDF

[7] Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[C]//Advances in neural information processing systems. 2012: 1097-1105. PDF

[8] 请问人工神经网络中的activation function的作用具体是什么？为什么ReLu要好过于tanh和sigmoid function? https://www.zhihu.com/question/29021768

[9] AF https://arxiv.org/pdf/1811.03378.pdf

本文有帮助？