Reinforce Learning

强化学习笔记。

K-摇臂赌博机

赌徒投币后选择一个摇臂，每个摇臂以一定概率吐出硬币。

算法需要最小化累计遗憾

\begin{align} R_T &= \sum_{i=1}^{T} \bigg(w_{opt} - w_{B(i)} \bigg) \\ &=Tw^* - \sum_{i=1}^{T} w_{B(i)} \end{align}

其中 $w_{B(i)}$ 是第 $i$ 次实验被选中臂的期望收益， $w^*$ 是最佳选择臂的收益。

基于规则

Explore

将所有机会平均分给么个摇臂

Exploit

按下目前最优的摇臂，如果多个同为最优，随机选择一个最优。

以上两种方法，是强化学习面临的『探索 - 利用窘境』（Exploration-Exploitation dilemma），折衷二者，以获得更优方案。

$\epsilon$ - greedy

以 $\epsilon$ 的概率进行探索；以 $1-\epsilon$ 的概率进行利用（选择 q_value 最大的摇臂）。

q_values[a] += (reward - q_values[a]) / counts[a]

Softmax

在 $\epsilon$ - greedy 基础上，1 - $\epsilon$ 的概率利用阶段，引入 softmax 使得：若某些摇臂的平均奖赏高于其他摇臂，则被选取的概率 $P$ 更高

$P(k)=\frac{e^{\frac{Q(k)}{\tau}}}{\sum_{i=1}^{K}e^{\frac{Q(i)}{\tau}}}$

其中 $Q(k)$ 记录当前摇臂的平均奖赏； $\tau > 0$ 称为温度，趋于 0 时仅利用，区域无穷大时仅探索。

1
2
3

scores = np.exp(q_values / softmax_temperature)
scores = scores / np.sum(scores)
best_arm = np.random.choice(range(len(q_values)), p=scores)

UCB

Upper Confidence Bound Algorithms

某个摇臂的奖赏样本越小，摇臂奖赏置信区间越大。UCB 根据摇臂奖赏置信区间上界（不同于 softmax 的奖赏均值），得到本次排序使用的值。

当两个摇臂均值相等，UCB 倾向探索次数较少、置信区间大的摇臂。

q_values_ucb = q_values + np.sqrt(1 / (counts + 0.001) * 2 * math.log(total_counts + 1.0))

UCB 是乐观的算法，对应 LCB 保守算法，选置信区间下界。

LinUCB

UCB 的拓展，利用上下文、User、Item 特征，建立线性模型预估：奖赏及其置信区间，选择置信区间上界最大的 Item 推荐，然后依据实际回报来更新线性关系的参数。

Thompson sampling

根据摇臂真实收益的 beta 概率分布，采样得到本次排序使用的值。

q_values[i] = np.random.beta(success_times[i], failure_times[i])

其中 beta 概率分布：

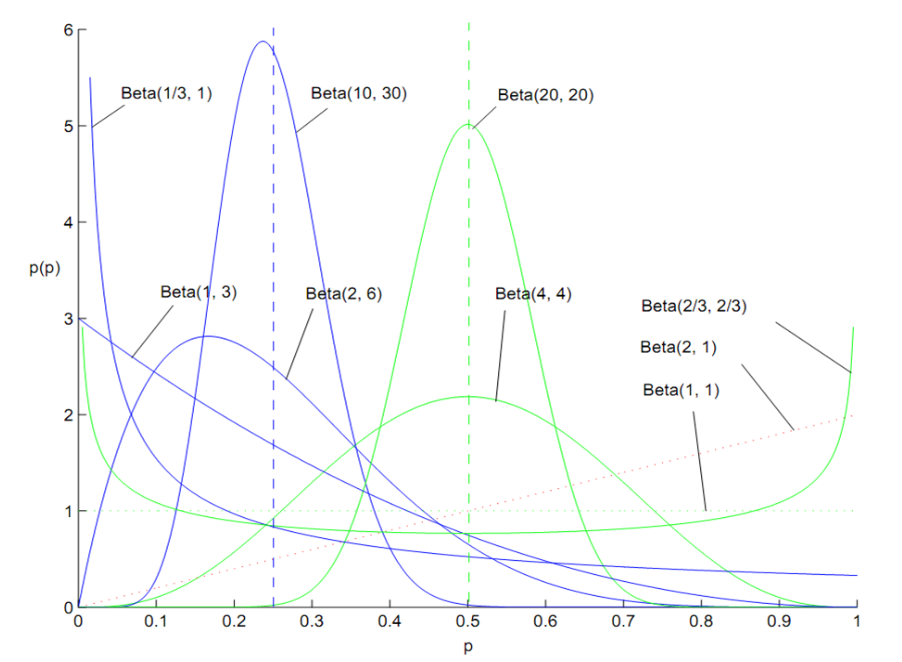
注：狄利克雷分布是 beta 分布的推广（抛硬币 -> 掷 n 面骰子）

有模型学习

假设任务对应的马尔科夫决策过程四元组 $E=<X,A,P,R>$ 已知，即模型已知，此时学习问题称为有模型学习。

Markov Decision Process

马尔可夫决策过程四元组 $E=<X,A,P,R>$ 中，四个变量已知。

那么可以对任意策略 $\pi$ 做评估，求累计奖赏和折扣累计奖赏：

V_T^\pi(x) = \mathbb E_\pi [\frac{1}{T} \sum_{t=1}^{T} r_t | x_0 = x] \\ V_\gamma^\pi(x) = \mathbb E_\pi [\frac{1}{T} \sum_{t=1}^{T} \gamma^t r_t | x_0 = x] \\

因此，也可以对策略 $\pi$ 进行改进、评估。

免模型学习

现实世界中，环境的转移概率、奖赏函数往往难以得知，甚至很难知道环境中一共有多少状态。若学习不依赖于环境建模，则称为免模型学习。

蒙特卡洛强化学习方法

蒙特卡洛方法（MC）又称模拟统计方法，通过随机数来解决计算问题，如通过洒豆子估算圆形的面积。

蒙特卡洛强化学习，通过多次采样，然后求平均累计奖赏来作为期望累积奖赏的近似。然后借鉴 \epsilon - 贪心法，在下一步执行策略。

On-Policy 同策略蒙特卡洛强化学习：

Off-Policy 异策略蒙特卡洛强化学习：（在策略评估时引入贪心策略，在策略改进时改进原始策略）

$$ Q(s_t,a_t) = Q(s_t,a_t) + \alpha [R - Q(s_t, a_t)] $$

TD 时序差分学习方法

即 Temporal Difference Learning (Sutton 1988)，可以避免蒙特卡洛方法需要在一个完整的采样轨迹完成后对所有状态-动作对进行更新的问题，通过增量更新的方法更新。

1-step TD 更新公式如下：

$Q_{t+1}(s_t, a_t) = Q_t(s_t, a_t) + \alpha [r_{t+1} + \gamma Q_t(s_{t+1}, a_{t+1}) - Q_t(s_t, a_t)]$

其中 $V^\pi (s)$ 是在状态 $s$ 和策略 $\pi$ 时的累计奖赏； $s_t$ 是 $t$ 时刻的状态， $r_{t+1}$ 是在 $t+1$ 时刻的观察奖赏。

蒙特卡洛方法可以看作是 max-step TD。

On-policy / Off-policy 学习方法

on-policy(同策略)：要learn的agent和环境互动的agent是同一个时，对应的policy。

off-policy(异策略)：要learn的agent和环境互动的agent不是同一个时，对应的policy。

DQN 使用 replay memory 采样而并非使用当前策略，所以是 off-policy。

QLearning 更新 Q 函数时，使用使用贪心策略。

PPO / TRPO

是 off-policy 的改进，通过 importance sampling 解决问题：求解期望值的样本数据由另一个概率分布产生，充分利用已观测数据。

Q-Learning

Q-Learning (Watkins 1989) 是一种 TD 方法。

基于值表（Tabular）的方法：
1. 用任意值初始化值表 $Q(s, a)$
2. 每个 episode 迭代：
  1. 初始化状态 $s$
  2. 每个 step 迭代：
    1. 根据一定的策略 $\pi$ （如 $\epsilon-greedy$ ）从值表 $Q(s, a)$ 中选取行动 $a=\pi(s)$
    2. 执行 $a$ ，观察奖赏 $r$ 和后续状态 $s'$
    3. 用 TD 方法更新 $Q(s, a)$ 和 $s$ ，直到 $s$ 为终止状态：
    \begin{align} Q(s,a) &\leftarrow Q(s,a) + \alpha[r + \gamma \max_{a'}Q(s',a') - Q(s,a)]\\ s &\leftarrow s' \end{align}

其中 Q 是动作效用函数，根据当前状态 $S$ 和行动 $A$ 给出累计期望收益评分，这个评分将用于指导下一步行动； $\gamma$ 是折扣系数； $\alpha$ 是学习率； $r$ 是奖赏；这里用 $\epsilon-greedy$ 方法进行探索和利用。

简单的说，TD 更新方法为：

新 Q(s, a) \leftarrow 老 Q(s, a) + \alpha * [现实\max_{a'} Q(s', a') - 老 Q(s, a)]

基于函数的训练方法：\begin{align} \theta_{i+1} &= \theta_i + \alpha (Y_i^Q - Q(s,a;\theta_i))\Delta_{\theta_i} Q(s,a;\theta_i)\\ Y_i^Q &\equiv r' + \gamma \max_{a'} Q(s', a';\theta_i) \end{align}

可用于推荐系统 [0.1]

Flappy Bird 例子知乎

Stanford Lecture Youtube

Sarsa

DQN Deep Q-Network

Human-level Control through Deep Reinforcement Learning 2015 PDF

是 Q-learning 的变体，改进点：

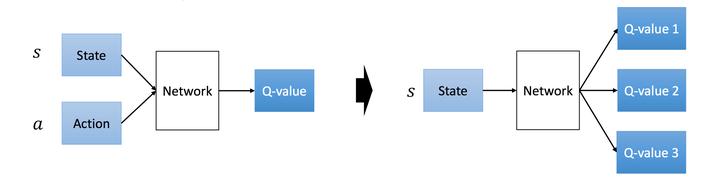
利用深度卷积神经网络拟合 $Q(s, a)$ 函数，替代值表；
利用经验回放进行学习；
独立设置了 target network 来单独处理时间差分算法中的 TD 偏差。

类型：model free（无环境模型）, off-policy（产生行为的策略和进行评估的策略不一样），value based方法，即只有一个值函数网络（critict），action space 离散且维度不高

https://zhuanlan.zhihu.com/p/91685011

Deep Q-Learning (Atari)

Playing Atari with Deep Reinforcemnet Leaning, Deepmind 2013 PDF

Value-based 方法，解决 Q-learning 值表方法的局限性，预测未出现的状态，用神经网络函数数拟合 Q：

$Q(s,a;\theta) \approx Q^*(s,a)$

以游戏画面（88x88x1）为输入，经过 AlexNet 得到状态向量 $s \in S$ ，动作空间 $a \in {0, 1} $ 是摇杆方向（左右）。输入图像经过两个 CNN 两个 FC ，输出摇杆方向。
在每一步结束后，利用经验回放（experience replay）进行参数学习，增加数据利用，减少迭代次数。（没有用 TD-Gammon 方法）

损失函数定义：

\begin{align} L_i(\theta_i) &= \mathbb{E}_{s,a \sim \rho(\cdot)} \bigg[\big(Y_i^Q - Q(s,a;\theta_i)\big)^2\bigg]\\ Y_i^Q &\equiv \mathbb{E}_{s'\sim \epsilon} \big[r + \gamma \arg\max_{a'} Q(s',a';\theta_{i-1})|s,a\big] \end{align}

其中 $\rho(s, a)$ 是关于 s 和 a 的概率分布； $y_i$ 是第 i 轮迭代的 TD-目标函数。

DQN

Double Q-Learning

Deep Reinforcement Learning with Double Q-Learning, Deepmind, Google 2010 PDF

通过神经网络预测 Qmax 有误差，每次向着最大误差的 Q现实改进神经网络，因为这个 Qmax 导致了 overestimate。而 Double DQN引入一个 Target-Netwrok 来减少最大误差的影响。

TD-目标函数 $Y_t^{DoubleQ}$ 改为：

\begin{align} Y_t^Q &\equiv r_{t+1} + \gamma \max_{a} Q(s_{t+1},a;\theta_t)\\ Y_t^{DoubleQ} &\equiv r_{t+1} + \gamma Q(s_{t+1},\arg \max_{a} Q(s_{t+1},a;\theta_t);\theta'_t)\\ \end{align}

DPG

Deterministic Policy Gradient Algorithms, 2014 PDF

DRL 解决了 Atari 中低维、离散动作空间的奖赏问题，即 $\arg\max_aQ(s,a)$ ，是 value-based 方法。然而在连续空间 value-based 方法动作空间太大，算法很难收敛。于是 DPG 引入了 policy-gradient，直接求解 policy，通过优化 policy 的参数来 $\max(Q)$ 。

DDPG

Continuous control with deep reinforcment learning, Deepmind, Google, ICLR 2016 PDF

一种 actor-critic 方法，输出具体行为，用于连续动作的预测。

类型：model free（无环境模型），off-policy，既有值函数网络(critic)，又有策略网络(actor)。

借鉴 DQN，使用目标网络和经验回放。

critic

$Q(s,a;w)$

critic target

$Q(s,a;w^-)$

Actor

$a = \pi(s;\theta)$

Actor target

$a = \pi(s;\theta^-)$

https://wanjun0511.github.io/2017/11/19/DDPG/

Actor Critic

动机：使用神经网络预估对 s 采取行动 a 的 reward，使得 reward 更稳定，加速 policy gradien 训练速度。

Critic：参数化行为价值函数 $Q_W(s, a)$

Actor：按照 Critic 部分得到的价值引导策略函数 $\pi_\theta(s,a)$ 参数 θ 的更新

其中Critic通过线性近似的TD(0)更新w，Actor通过策略梯度更新θ，具体算法流程如下：

策略不需用 e-greedy 搜索，而是根据 $\theta$ 得到，因为梯度变化而尝试更多的行为，通过 $\alpha$ 控制策略更新的平滑度。.

论文《Off-Policy Actor-Critic》从 on-policy 扩展到 off-policy

A3C

Asynchronous Advantage Actor-Critic PDF

改进 AC，异步训练、多个智能体共同探索。

模仿学习

通过借助专家决策过程的范例，加速学习过程。

直接模仿学习

首先获取人类专家的决策轨迹数据 \{\tau_1, \tau_2, …, \tau_m\}，每条轨迹包括状态和动作序列

$\tau_i = \langle s_1^i, a_1^i, s_2^i, s_2^i, ..., s_{n_i+1}^i \rangle$

其中 $n_i$ 为第 $i$ 条轨迹中的转移次数

我们可以把 $s$ 作为输出， $a$ 作为输出，通过有监督学习以下数据集，得到一个初始化的策略模型

$D=\{(s_1, a_1), (s_2, a_2), ..., (s_{\sum^m_{i=1} n_i}, a_{\sum_{i=1}^m n_i})\}$

然后把学得的策略模型作为强化学习的输入

逆强化学习

TODO

总结

强化学习算法分类：

MDP 的转移函数、奖赏函数是否已知：有模型 / 免模型

Q/Value 函数更新方法：值表 / TD

Actor/Policy 函数更新方法：policy gradient

Actor：离散 / Linear / DNN（policy function approx），一般通过 policy gradient 更新

Critic：无 / DNN（value function approx），一般通过 TD 更新

Target Network：无 / Actor / Critict / Actor & Critict

学习 Actor 和环境互动 Actor 是否一致：On-policy / Off-policy

经验回放：有/无

模拟器：有/无

奖赏塑形：有（引入先验知识）/无

Reference

[1] 《机器学习》周志华

[2] Bandit算法与推荐系统 http://geek.csdn.net/news/detail/195714

[3] 深度强化学习（Deep Reinforcement Learning）入门：RL base & DQN-DDPG-A3C introduction 知乎

[4] 阿里和京东的增强学习, 能比Learning to Rank好一倍，Dong Wang URL

[5] 『干货』深度强化学习与自适应在线学习的阿里实践 URL

Code

greedy / $\epsilon$ -greedy / UCB / Thompson / Sampling

# encoding = 'utf-8'

import numpy as np
import matplotlib.pyplot as plt
import math

num_of_bandits = 10
num_of_arms = 10
num_of_pulls = 10000
epsilon = 0.3
min_temp = 0.1
softmax_temperature = 0.1
decay_rate = 0.999

def pick_arm(q_values, counts, strategy, success, failure):
    global epsilon
    if strategy == "random":
        return np.random.randint(0, len(q_values))

    # pick best (if multiple best, randomly pick one)
    if strategy == "greedy":
        best_arms_value = np.max(q_values)
        best_arms = np.argwhere(q_values == best_arms_value).flatten()
        return best_arms[np.random.randint(0, len(best_arms))]

    if strategy == "egreedy" or strategy == "egreedy_decay":
        if strategy == "egreedy_decay":
            epsilon = max(epsilon * decay_rate, min_temp)

        if np.random.random() > epsilon:
            best_arms_value = np.max(q_values)
            best_arms = np.argwhere(q_values == best_arms_value).flatten()
            return best_arms[np.random.randint(0, len(best_arms))]
        else:
            return np.random.randint(0, len(q_values))

    if strategy == "softmax":
        scores = np.exp(q_values / softmax_temperature)
        scores = scores / np.sum(scores)
        best_arm = np.random.choice(range(len(q_values)), p=scores)
        return best_arm

    if strategy == "ucb":
        total_counts = np.sum(counts)
        q_values_ucb = q_values + np.sqrt(1.0 / (counts + 0.001) * 2 * math.log(total_counts + 1.0))
        best_arms_value = np.max(q_values_ucb)
        best_arms = np.argwhere(q_values_ucb == best_arms_value).flatten()
        return best_arms[np.random.randint(0, len(best_arms))]

    if strategy == "thompson":
        sample_means = np.zeros(len(counts))
        for i in range(len(counts)):
            sample_means[i] = np.random.beta(success[i] + 1, failure[i] + 1)
        return np.argmax(sample_means)


fig = plt.figure()
ax = fig.add_subplot(111)
for strategy in ["greedy", "random", "egreedy", "egreedy_decay", "softmax", "ucb", "thompson"]:

    best_arm_counts = np.zeros((num_of_bandits, num_of_pulls))

    for i in range(num_of_bandits):
        arm_means = np.random.rand(num_of_arms)
        best_arm = np.argmax(arm_means)

        q_values = np.zeros(num_of_arms)
        counts = np.zeros(num_of_arms)
        success = np.zeros(num_of_arms)
        failure = np.zeros(num_of_arms)

        for j in range(num_of_pulls):
            a = pick_arm(q_values, counts, strategy, success, failure)

            reward = np.random.binomial(1, arm_means[a])
            counts[a] += 1.0
            q_values[a] += (reward - q_values[a]) / counts[a]

            success[a] += reward
            failure[a] += (1 - reward)
            best_arm_counts[i][j] = counts[best_arm] * 100.0 / (j + 1)

    ys = np.mean(best_arm_counts, axis=0)
    xs = range(len(ys))
    ax.plot(xs, ys, label=strategy)

plt.xlabel('Steps')
plt.ylabel('Optimal pulls')

plt.tight_layout()
plt.legend()
plt.ylim((0, 110))
plt.show()