在线学习方法概述

Posted on

推荐系统算法常常用到逻辑回归算法，而传统的批量学习算法如 SGD 无法应对大规模、高维的数据集和实时数据流。为了解决这个问题，在线最优化算法如 TG [1]、FOBOS [2]、RDA [3]、FTRL [4,5,6] 应运而生，下面将介绍、对比这些算法。

TODO

TG

L1 正则化在 online 不能产生较好的稀疏性，而稀疏性对于高维特征向量以及大数据集又特别的重要。为解决这个问题，John Langford 等人在 2009 年提出 Truncated Gradient [1]。

SGD

对于传统的在线学习方法 SGD，有更新规则

wi+1=wi−ηg(wi,zj)w_{i+1}=w_i - \eta g(w_i, z_j)

其中 zj=(xj,yj)z_j = (x_j, y_j) ， g(a,b)g(a,b) 是 L(a,b)L(a,b) 对于 aa 的次梯度。

然而，SGD 方法无法满足稀疏性

Simple Coefficient Rounding

简单截断法。为了稀疏性，基于 GD，在每 K 次迭代，应用下面的规则，把小的 ww 置 0。

wi+1=T0(wi−ηgt,θ)w_{i+1} = T_0\big(w_i - \eta g_t, \theta\big)

其中 T0T_0 是分段函数

T0(vj,θ)={0if ∣vj∣≤θvjotherwiseT_0(v_j, \theta) = \begin{cases} 0 & \text{if } |v_j| \le \theta \\ v_j & \text{otherwise} \end{cases}

Truncated Gradient

改进了简单截断法中，每 K 步把 wiw_i 置 0 太激进的问题，改进了有更新规则

wi+1=T1(wi−ηgt,ηλ,θ)w_{i+1} = T_1 \big(w_i - \eta g_t, \eta \lambda, \theta \big)

其中 T1T_1 定义

T1(vj,α,θ)={max(0,vj−α)if vj∈[0,θ]min(0,vj+α)if vj∈[−θ,0]vjotherwiseT_1(v_j, \alpha, \theta) = \begin{cases} \max(0, v_j - \alpha) &\text{if } v_j \in [0, \theta] \\ \min(0, v_j + \alpha) &\text{if } v_j \in [-\theta, 0] \\ v_j &\text{otherwise} \end{cases}

简单截断法的 T0T_0 与 TG 的 T1T_1 的对比

tg

FOBOS

Sub-gradient

定义 gg 为 ff 的次梯度：

f(z)−f(x)≥gT(z−x)f(z)-f(x) \ge g^T(z-x)

或

wt+1=wt−ηtgtfw_{t+1}=w_t - \eta_t g_t^f

例，f(x)=∣x∣f(x)=|x| 在 0 处的 sub-gradient∈[−1,1]\text{sub-gradient} \in [-1, 1]

stanford

Projected Sub-gradient

w_{t+1}= \Pi_\Omega (w_t - \eta_t g_t^f )=\underset {w \in \Omega} {\arg \min} \bigg\{ \bigg| \bigg| w - (w_t - \eta_t g_t^f)\bigg|\bigg|^2_2 \bigg\}

其中 ΠΩ(w)\Pi_\Omega(w) 是 ww 到 Ω\Omega 的欧几里得投影距离。

illinois oxford

FOBOS

前向后向切分，Forward-Bakcward Splitting，又称 FOLOS (Forward Looking Subgradients)，由 John Duchi 等人在 2009 提出 [2]，解决凸优化问题如下

f(w)+r(w)f(w)+r(w)

权重更新分为两部分

\begin{align} w_{t+\frac{1}{2}} &= w_t - \eta_t g_t\\ w _{t+1} &= \underset{w}{\arg \min} \bigg\{\frac{1}{2} ||w-w_{t+\frac{1}{2}}||^2 + \eta_{t+\frac{1}{2}}r(w) \bigg\} \end{align}

第一项是标准梯度下降；第二项是微调，处理正则化，产生稀疏性。rr 是正则函数。

当 wt+1w_{t+1} 有最优解时，有

\textbf{0} \in \partial \bigg\{\frac{1}{2} \big|\big|w-w_{t+\frac{1}{2}} \big|\big|^2 + \eta_{t+\frac{1}{2}} r(w) \bigg\}

由 wt+12=wt−ηtgtfw_{t+\frac{1}{2}} = w_t - \eta_t g_t^f ，上式可化简为

\textbf 0 \in w_{t+1} - w_t + \eta_t g_t^f + \eta_{t+\frac{1}{2}} \partial r(w_{t+1}) \\ \textbf 0= w_{t+1} - w_t + \eta_t g_t^f + \eta_{t+\frac{1}{2}} g_{t+1}^r

最终，得到更新公式

wt+1=wt−ηgtf−ηt+12gt+1rw_{t+1} = w_t - \eta g_t^f - \eta_{t+\frac{1}{2}} g_{t+1}^r

其中 gtf∈∂f(wt)g_t^f \in \partial f(w_t) ， gt+1r∈∂r(wt+1)g_{t+1}^r \in \partial r(w_{t+1})

可以看出，更新公式不仅和当前的状态 wtw_t 相关，和迭代后的 r(wt+1)r(w_{t+1}) 相关，因此改算法称为前向后向切分。

当 rr 是 ℓ1\ell_1 ，在 [2] 的 5.1 章节描述了对应的 derived algorithm。

RDA

RDA 是 Simple Dual Averaging Scheme 的一个扩展，由 Lin Xiao 在 2009 发表 [3]。

更新策略为

w_{t+1}=\underset {w}{\arg \min} \bigg\{ \frac{1}{t} \sum_{r=1}^t + r(w) + \frac{\beta_t}{t}h(w) \bigg\}

其中， <Gr,w><G_r,w> 表示梯度 GrG_r 对 ww 的积分平均值；rr 是正则项； hh 是辅助的严格凸函数； {βt∣t≥1}\{\beta_t|t\ge1\} 是一个非负且非自减序列。

RDA 更新策略，最小化：第一项，之前所有梯度的平均值（dual average）；第二项，正则项；第三项，额外正则项。

FTRL-Proximal

FTRL_Proximal 是 McMahan 在 2010 提出 [4]，在 [5] 与 FOBOS RDA 对比，在 [6] 介绍了 Google FTRL 工程实践。

一般 Online Gradient Descent (SGD) 更新公式为

wt+1=wt−ηtGtw_{t+1} = w_t - \eta_t G_t

其中 ηt\eta_t 是非递减的学习率，GtG_t 是梯度。

FTRL 综合了 FOBOS 和 RDA，更新公式为

w_{t+1} = \underset{w}\arg\min \bigg\{ G_{1:t} \cdot w + \frac{1}{2} \sum_{s=1}^t \sigma_s ||w-w_s||_2^2 + \lambda_1 ||w||_1\bigg\}

其中 σs=1/ηt\sigma_s = 1 / \eta_t，G1:t=∑i=0tGiG_{1:t}=\sum_{i=0}^{t} G_i

为简化计算，重写更新公式为

argmin{(G1:t−∑s=1tσsws)⋅w+1ηt∣∣w∣∣22+λ1∣∣w∣∣1+(const)}\arg \min \bigg\{ \big(G_{1:t} - \sum_{s=1}^t \sigma_s w_s \big) \cdot w + \frac{1}{\eta_t}||w||^2_2 + \lambda_1 ||w||_1 + (const) \bigg\}

上一步记录 zt−1=G1:t−1−∑s=1t−1σswsz_{t-1} = G_{1:t-1} - \sum_{s=1}^{t-1} \sigma_s w_s

下一步更新 zt=zt−1+gt(1/ηt−1/ηt−1)wtz_{t} = z_{t-1} +g_t (1/\eta_t - 1/\eta_{t-1})w_t

推出 wt+1w_{t+1} 的封闭解？

wt+1={0,if ∣zt,i∣≤λi−ηt(zt,i−sgn(zt,i)λ1),otherwise w_{t+1} = \begin{cases} 0, &\text{if } |z_{t,i}| \le \lambda_i \\ -\eta_t (z_{t,i} - sgn(z_{t,i})\lambda_1), &\text{otherwise } \end{cases}

其中每个特征维度，有着不同的学习率，特征变化大的维度学习率下降得快

ηt,i=αβ+∑s=1tGs,i2\eta_{t,i} = \frac{\alpha}{\beta + \sqrt{\sum_{s=1}^t G_{s,i}^2}}

算法实现 https://github.com/fmfn/FTRLp

算法流程

FTRL_Proximal

与 FOBOS 不同，FTRL 与 RDA 在估计梯度时使用了历史累计梯度信息，而不仅仅是上一轮梯度。

在 [5] 提出把全局学习率改成每个坐标自适应学习率，AUC 提升1%。

横向对比

img

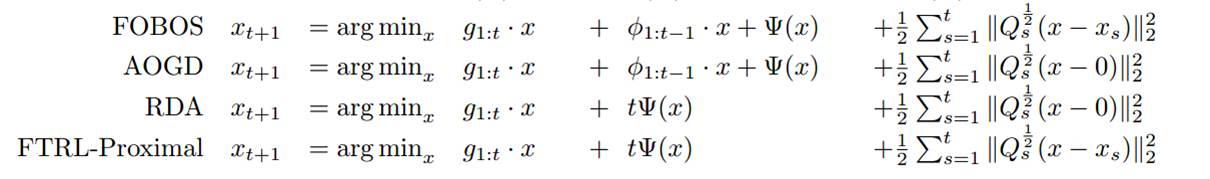
其中 Ψ\Psi 是非平滑凸函数，如 L1 正则项。QsQ_s 是学习率。

其中TG截断比较武断；FOBOS能获得较好的精度，但是稀疏性较差；RDA算法会在牺牲一定的精度条件下，获得较好的稀疏性；而FTRL算法技能提高 OGD（online-gradient-descent）的精确度，又能获得更好的稀疏性。

Appendix

凸函数定义

f(tX_1 + (1-t)X_2) \le t f(X_1) + (1-t)f(X_2) \\ \forall X_1, X_2 \in \mathbb C, 0 \le t \le 1

严格凸函数

f(tX_1 + (1-t)X_2) \lt t f(X_1) + (1-t)f(X_2) \\ \forall X_1, X_2 \in \mathbb C, 0 \lt t \lt 1

一个函数是凸函数的充要条件是它存在最优解。

Proximal 方法

proximal方法的思想可以看作是来源于梯度投影策略：相比起用整体次梯度来迭代求解，先基于损失函数做梯度下降，得到“无约束中间解”，再其投影回去约束区域（L1 L2）中。

wt+1=argminw{(w−(wt−η∇l(wt)))2+λ∣w∣}w_{t+1} = \arg \min_w \bigg\{ \bigg(w - \big(w_t - \eta \nabla l(w_t)\big)\bigg)^2 + \lambda |w| \bigg\}

忽略常数项 (η∇l(wt))2(\eta\nabla l(w_t))^2 有

wt+1=argminw{2η∇l(wt)(w−wt)+(w−wt)2+λ∣w∣}w_{t+1} = \arg \min_w \bigg\{ 2\eta \nabla l(w_t)(w - w_t) + (w - w_t)^2 + \lambda |w| \bigg\}

其中 Proximal 项 (w−wt)2(w-w_t)^2 也称为 local bregman divergence；另一种 Proximal 项 ∣∣x∣∣22||x||_2^2 称为 global proximal function（RDA 采用）。

求得解析解

wt+1={xt−η∇l(wt)−λ2,if xt−η∇l(xt)>λ2xt−η∇l(wt)−λ2,if xt−η∇l(xt)<−λ20,if ∣xt−η∇l(xt)∣≤λ2w_{t+1} = \begin{cases} x_t - \eta \nabla l(w_t) - \frac{\lambda}{2}, & if\ x_t - \eta\nabla l(x_t) \gt \frac{\lambda}{2} \\ x_t - \eta \nabla l(w_t) - \frac{\lambda}{2}, & if\ x_t - \eta\nabla l(x_t) \lt -\frac{\lambda}{2} \\ 0, &if\ |x_t - \eta\nabla l(x_t)| \le \frac{\lambda}{2} \end{cases}

Reference

[1] Langford, John, Lihong Li, and Tong Zhang. “Sparse online learning via truncated gradient.” Journal of Machine Learning Research 10.Mar (2009): 777-801. PDF

[2] Duchi, John, and Yoram Singer. “Efficient online and batch learning using forward backward splitting.” Journal of Machine Learning Research 10.Dec (2009): 2899-2934. PDF

[3] Xiao, Lin. “Dual averaging methods for regularized stochastic learning and online optimization.” Journal of Machine Learning Research 11.Oct (2010): 2543-2596. PDF

[4] McMahan, H. Brendan, and Matthew Streeter. “Adaptive bound optimization for online convex optimization.” arXiv preprint arXiv:1002.4908 (2010). PDF

[5] McMahan, Brendan. “Follow-the-regularized-leader and mirror descent: Equivalence theorems and l1 regularization.” Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics. 2011. PDF

[5] McMahan, H. Brendan, et al. “Ad click prediction: a view from the trenches.” Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2013. PDF

[6] 在线最优化求解(Online Optimization) 冯扬 PDF

[7] 简谈L0,L1和L2 modkzs http://modkzs.github.io/2016/02/22/简谈L0-L1和L2/

[8] TRUNCATED GRADIENT (TG) 算法简介 ZHANG RONG https://zr9558.com/2016/01/12/truncated-gradient/

[9] FTRL总结 https://zhuanlan.zhihu.com/p/35449814

[10] Line Search with Python https://nlperic.github.io/line-search/

[11] https://github.com/Angel-ML/angel/

[12] 只需20分钟的十亿规模模型训练——试试Spark on Angel的FTRL

[13] LR+FTRL算法原理以及工程化实现 https://zhuanlan.zhihu.com/p/55135954
本文有帮助？