dnn-tricks

Posted on

DNN 如何调优？

欠拟合

  • 增加模型深度：ResNet20 -> ResNet50

  • 微调结构：更小的 feature map & pooling size

  • 更换复杂网络：AlexNet -> ResNet -> …

  • DeepCTR 模型使用高阶特征交叉（DCN、xDeepFM）

  • 梯度弥散：BatchNorm

过拟合

  • 数据预处理：不平衡类别；异常值剔除；PCA / ZCA Whitening 或者 BatchNorm；加入噪音增强模型鲁棒性

  • 数据扩增：加入噪音；图片旋转、平移、剪裁、颜色、调色；SMOTE；合成样本；使用外部数据

  • 迁移学习：在 ImageNet VGG 基础上训练，根据数据分布决定是否冻结权重

  • 正则化：L1、L2

  • Dropout

  • 早停

  • 多目标学习：ESMM

  • 半监督学习：无标注样本假设（平滑假设、聚类假设、流形假设）

  • 迁移学习

  • 多模态学习

  • 对抗训练：GAN，合成对抗样本

精度提升

  • 初始化：全0、随机、he_normal() mean=0,var=sqrt(2/fan_in)mean=0,var=sqrt(2/fan\_in)、glorot_normal() mean=0,var=sqrt(2/(fan_in+fan_out))mean=0,var=sqrt(2 / (fan\_in + fan\_out))
  • 学习率：微调，Adagrad Adam 自适应学习率的优化方法
  • 激活函数
  • 损失函数
  • 组合模型：Bagging 或 Boosting；CV；同一模型多次初始化训练
  • 样本不平衡：负样本降采样；设置类权重；2-stage 分类任务；单独在少数类别样本上微调
  • 特征工程：Embedding

附录

范数

损失函数中，正则项一般是参数的 Lp 距离。向量 x 的范数，指原点到 x 的距离。

L1最优化问题的解是稀疏性的, 其倾向于选择很少的一些非常大的值和很多的insignificant的小值. 而L2最优化则更多的非常少的特别大的值, 却又很多相对小的值, 但其仍然对最优化解有显著的贡献. 但从最优化问题解的平滑性来看, L1范数的最优解相对于L2范数要少, 但其往往是最优解, 而L2的解很多, 但更多的倾向于某种局部最优解.

L0范数本身是特征选择的最直接最理想的方案, 但如前所述, 其不可分, 且很难优化, 因此实际应用中我们使用L1来得到L0的最优凸近似. L2相对于L1具有更为平滑的特性, 在模型预测中, 往往比L1具有更好的预测特性. 当遇到两个对预测有帮助的特征时, L1倾向于选择一个更大的特征. 而L2更倾向把两者结合起来.

lp-balls

L0-范数

d=∑i=1n(xi0)10d=\sum_{i=1}^{n}\bigg(x_i^{0}\bigg)^{\frac {1}{0}}

向量中非零元素的个数

在 Sparse Coding 中, 通过最小化 L0 寻找最少最优的稀疏特征. 但难以优化, 一般转化成 L1 L2

L1-范数

曼哈顿距离

d=∑i=1n∣xi−yi∣d=\sum_{i=1}^{n}\bigg|x_i-y_i\bigg|

如计算机视觉中对比两张图片的不同像素点之和

L2-范数

欧几里得距离

d=∑i=1n(∣xi−yi∣2)12d=\sum_{i=1}^{n}\bigg(|x_i-y_i|^{2}\bigg)^{\frac {1}{2}}

Lp-范数

d=∑i=1n(∣xi−yi∣p)1pd=\sum_{i=1}^{n}\bigg(|x_i-y_i|^{p}\bigg)^{\frac {1}{p}}

无限范数距离

切比雪夫距离

d = \lim_{p \to \infty}\sum_{i=1}^{n}\bigg(|x_i-y_i|^{p}\bigg)^{\frac {1}{p}} = \max(|x_1-y_1|,…,|x_n-y_n|)

损失函数

0 - 1 损失函数

gold standard

L01(m)={0if m≥01elseL_{01}(m)=\begin{cases} 0 &\text{if } m \ge 0 \\ 1 &\text{else} \end{cases}

对数损失函数

Log Loss, cross entropy error

L(Y,P(Y∣X))=−logP(Y∣X)L(Y,P(Y|X))=-\log P(Y|X)

对 LR 而言, 把它的条件概率分布方程

P(Y=0∣X)=11+ewx+b,P(Y=1∣X)=1−P(Y=0∣X)P(Y=0|X)=\frac {1}{1+e^{wx+b}}, P(Y=1|X)=1-P(Y=0|X)

带入上式, 即可得到 LR 的对数损失函数

平方损失函数

Square Loss

L(Y,P(Y∣X))=∑i=1n(Y−f(X))2L(Y,P(Y|X))=\sum_{i=1}^{n}(Y-f(X))^2

其中 Y−f(X)Y-f(X) 表示残差, 整个式子表示残差平方和, Residual Sum of Squares

指数损失函数

Exponential Loss

L(Y,f(X))=e−Yf(X)L(Y,f(X))=e ^ {-Y f(X)}

如 Adaboost, 它是前向分步加法算法的特例, 是一个加和模型, 损失函数就是指数函数. 经过m此迭代之后, 可以得到

fm(x)=fm−1(x)+αmGm(x)f_m(x)=f_{m-1}(x)+\alpha_mG_m(x)

Adaboost 每次迭代的目标是最小化指数损失函数

arg minα,G=∑i=1Ne[−yi(fm−1(xi)+αG(xi))]{\arg\ \min}_{\alpha, G}=\sum_{i=1}^{N}e^{[-y_i(f_{m-1}(x_i)+\alpha G(x_i))]}

合页损失

Hinge Loss, 如 SVM

L(Y,f(X))=max(0,1−Y∗f(X)),Y={0,1}L(Y,f(X))=max(0,1-Y * f(X)), Y=\{0,1\}

含义是样本被正确分类且函数间隔大于1时,损失时0; 否则损失是 1−Yf(X)1-Y f(X). 当分类正确且确信度足够高时, 损失才是0, 对学习有更高的要求.

img

Huber 损失

常用于回归树。与比平方损失相比，它对 outlier 更加不敏感

对于回归问题

Lδ(a)={12a2for ∣a∣≤δ,δ(∣a∣−12δ)otherwise.L_{\delta}(a) = \begin{cases} \frac{1}{2} a^2 &\text{for } |a| \le \delta,\\ \delta \big( |a| - \frac{1}{2} \delta \big) &\text{otherwise.} \end{cases}

其中 ∣a∣=y−f(x)|a|=y-f(x)

对分类问题

Lδ(y,f(x))={12(y−f(x))2for ∣y−f(x)∣≤δ,δ∣y−f(x)∣−12δ2otherwise.L_{\delta}\big(y, f(x)\big) = \begin{cases} \frac{1}{2} \big(y-f(x)\big)^2 &\text{for } \big|y-f(x)\big| \le \delta,\\ \delta \big|y-f(x) \big| - \frac{1}{2} \delta^2 &\text{otherwise.} \end{cases}

下图是 huber loss（绿色）与平方损失（蓝色）的对比，来自 wiki

huber loss

正则化

Regulization or Penalization：

minw∈Θ1N∑i=lNL(yi,f(xi,w))+λJ(w){\min}_{w \in \Theta}\frac{1}{N}\sum_{i=l}^{N}L(y_i,f(x_i,w))+\lambda J(w)

其中第一项是经验风险, 第二项是正则化项。常见的正则项，通过 L0,L1,L2L_0,L_1,L_2 范数衡量参数 ww，有

J0(w)=∣{i:wi≠0}∣J_0(w) = \big|\{i:w_i \ne 0\}\big|

J1(w)=∑i∣wi∣J_1(w) = \sum_i |w_i|

J2(w)=12∣∣w∣∣2J_2(w) = \frac{1}{2} ||w||^2

其中 L2L_2 正则项最常用，因为它是凸函数，可以用梯度下降法求解。

而 L1L_1 正则项有特征选择功能，能够得到更加稀疏、更多 0 的解。可以用简单截断法，梯度截断法（TG, Truncated Gradient），ADMM 方法求解。

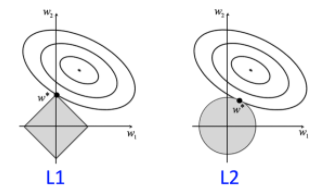
以 w∈R2w\in \mathbb R^2 为例，椭圆形是 loss 的损失等高线，灰色区域是约束区域，等高线与约束区域相交的地方，就是最优解。可以看出，L1 较 L2 有更大的概率在角处相交，得到稀疏解。

l1vsl2

Batch Norm

Internal Covariate Shift 定义：在深层网络训练的过程中，由于网络中参数变化而引起内部结点数据分布发生变化的这一过程被称作Internal Covariate Shift。

常见的方法有对每层输入做 Whitening，保留彼此不相关的特征（耗时），然后使其具有相同的均值和方差（同分布）：

1
2
3
4
5
6
# compute the SVD factorization of the data covariance matrix
U,S,V = np.linalg.svd(cov)
# decorrelate the data
Xrot = np.dot(X, U) 
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)

BN 改进了 Whitening 计算耗时的问题，退而求其次，对每个特征进行标准化，使其具有均值为0，方差为1的分布。

img

编辑距离

指两个字串之间，由一个转成另一个所需的编辑操作次数，包括 ：

Levenshtein距离：可以删除、加入、取代字符串中的任何一个字元

LCS（最长公共子序列）距离：只允许删除、加入字元

Jaro 距离：只允许字符转置

汉明距离：只允许取代字元

Jaccard 距离

J(A,B)=A∩BA∪BJ(A,B) = \frac{A \cap B}{A \cup B}

余弦相似性

dist(A,B)=cosθ=A⋅B∣∣A∣∣×∣∣B∣∣dist(A, B)=\cos\theta =\frac{A \cdot B}{||A||\times||B||}

余弦距离衡量两个向量的夹角。当向量是用户评分时，可以自动做评分尺度归一。比如 dist((1,1)(3,3))==dist((1,1),(5,5))dist((1,1) (3,3)) == dist((1,1),(5,5))

0度角的余弦值是1，而其他任何角度的余弦值都不大于1；并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。这结果是与向量的长度无关的，仅仅与向量的指向方向相关。余弦相似度通常用于正空间，因此给出的值为0到1之间。

本文有帮助？