Google用户付费预估深度模型笔记

Posted on 2020-09-17

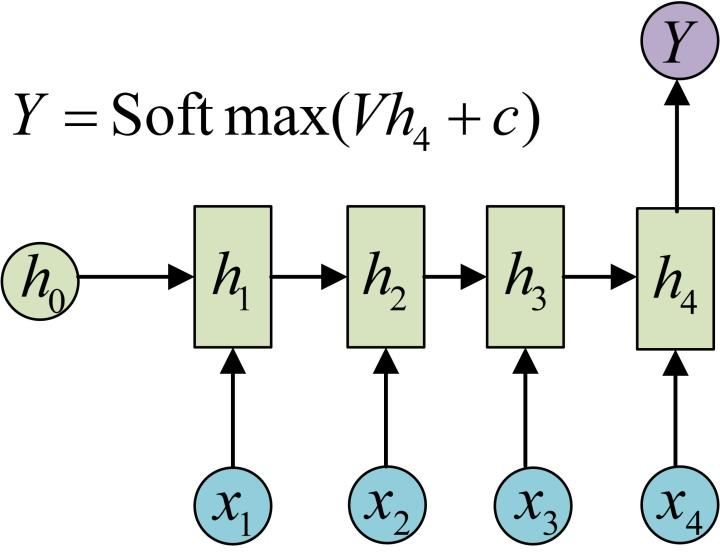
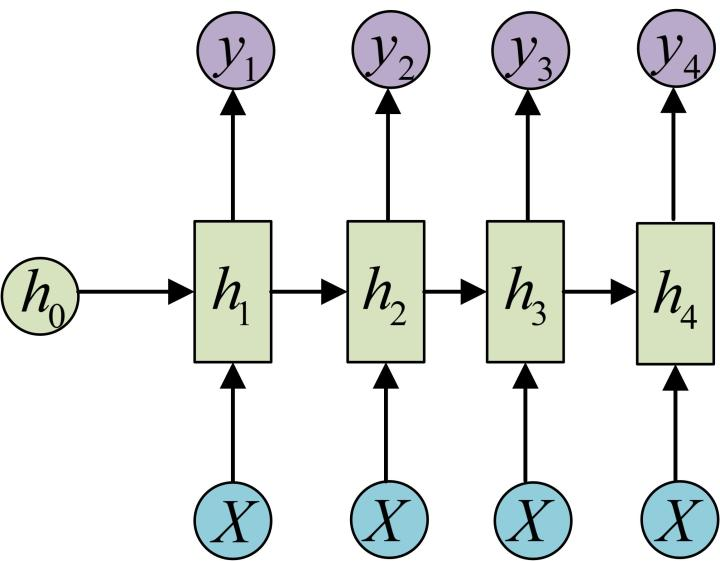
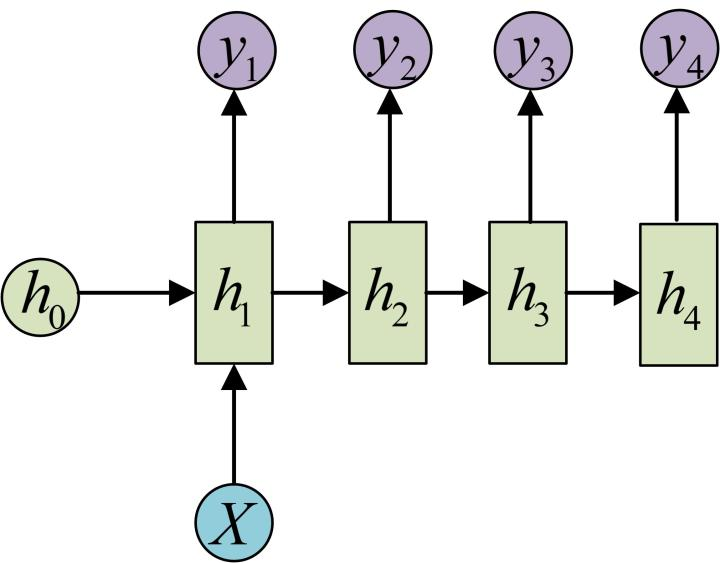
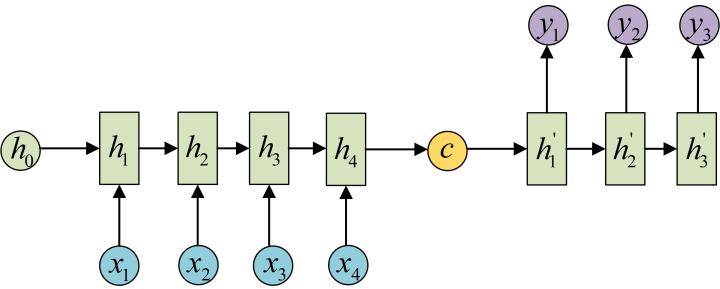
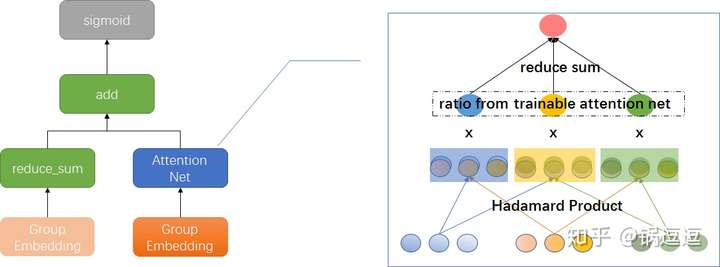
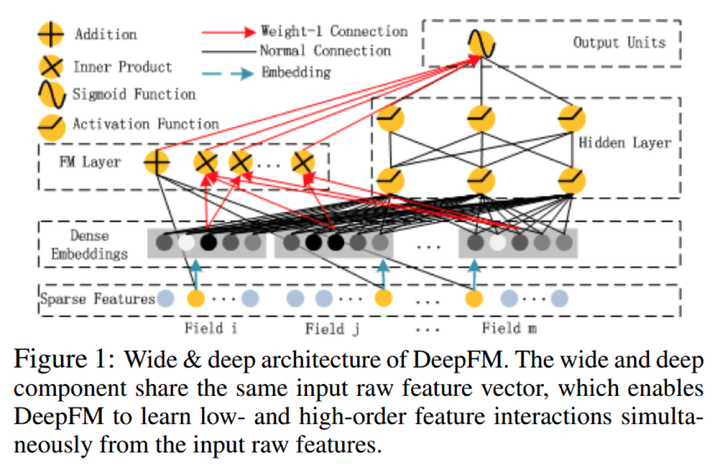
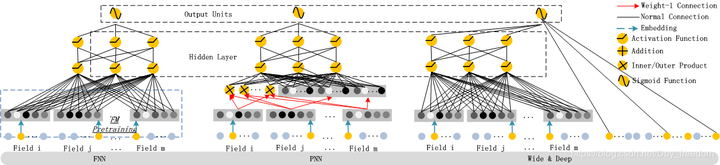
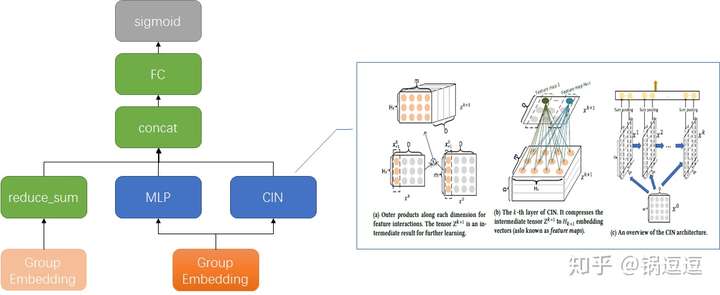
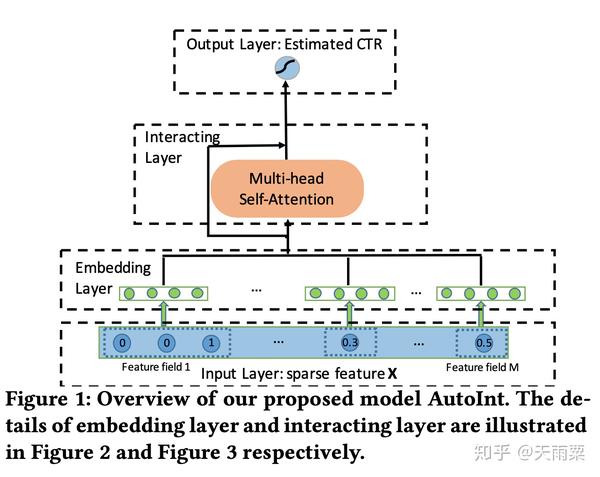
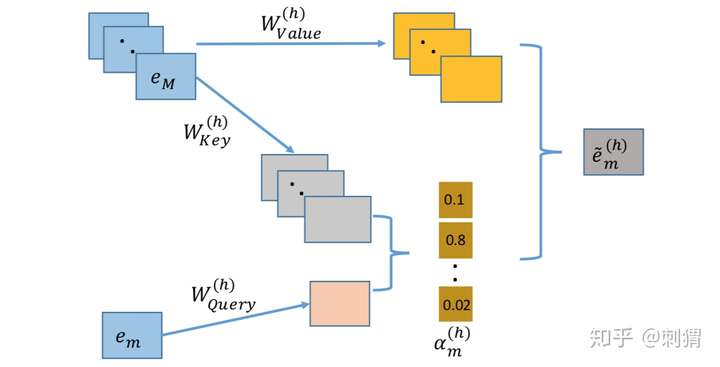
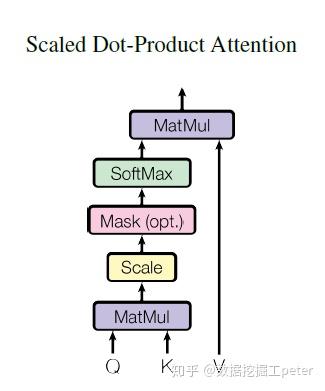
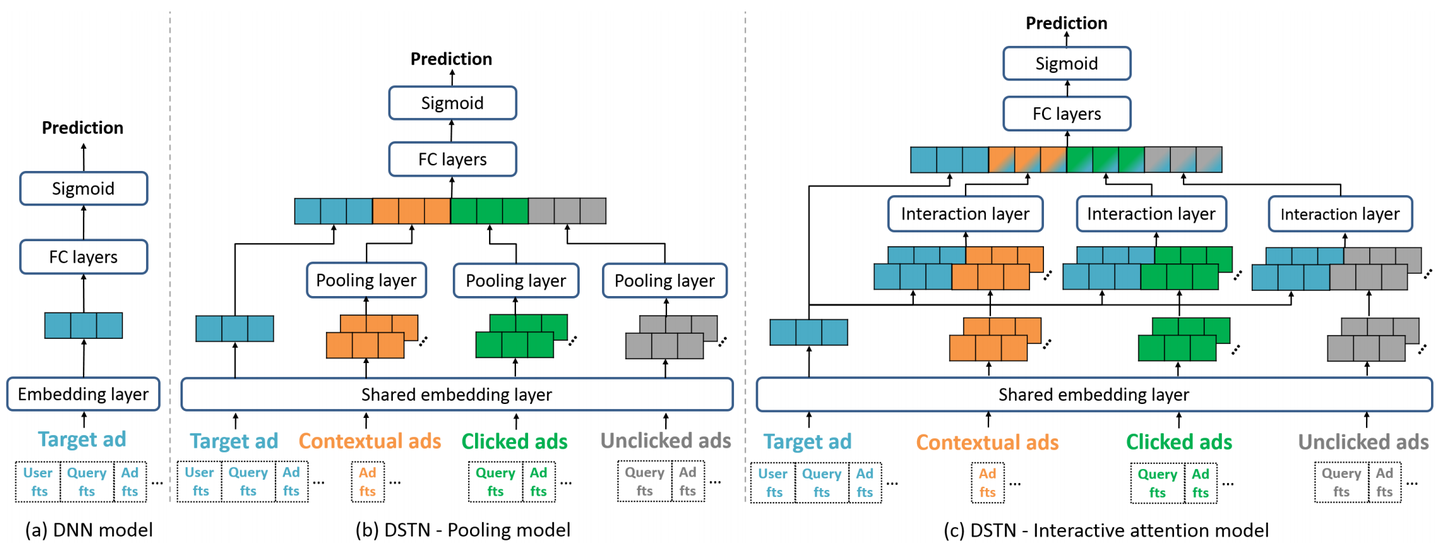
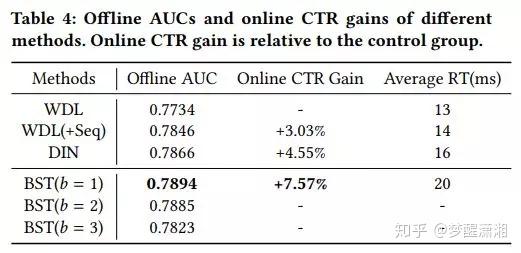
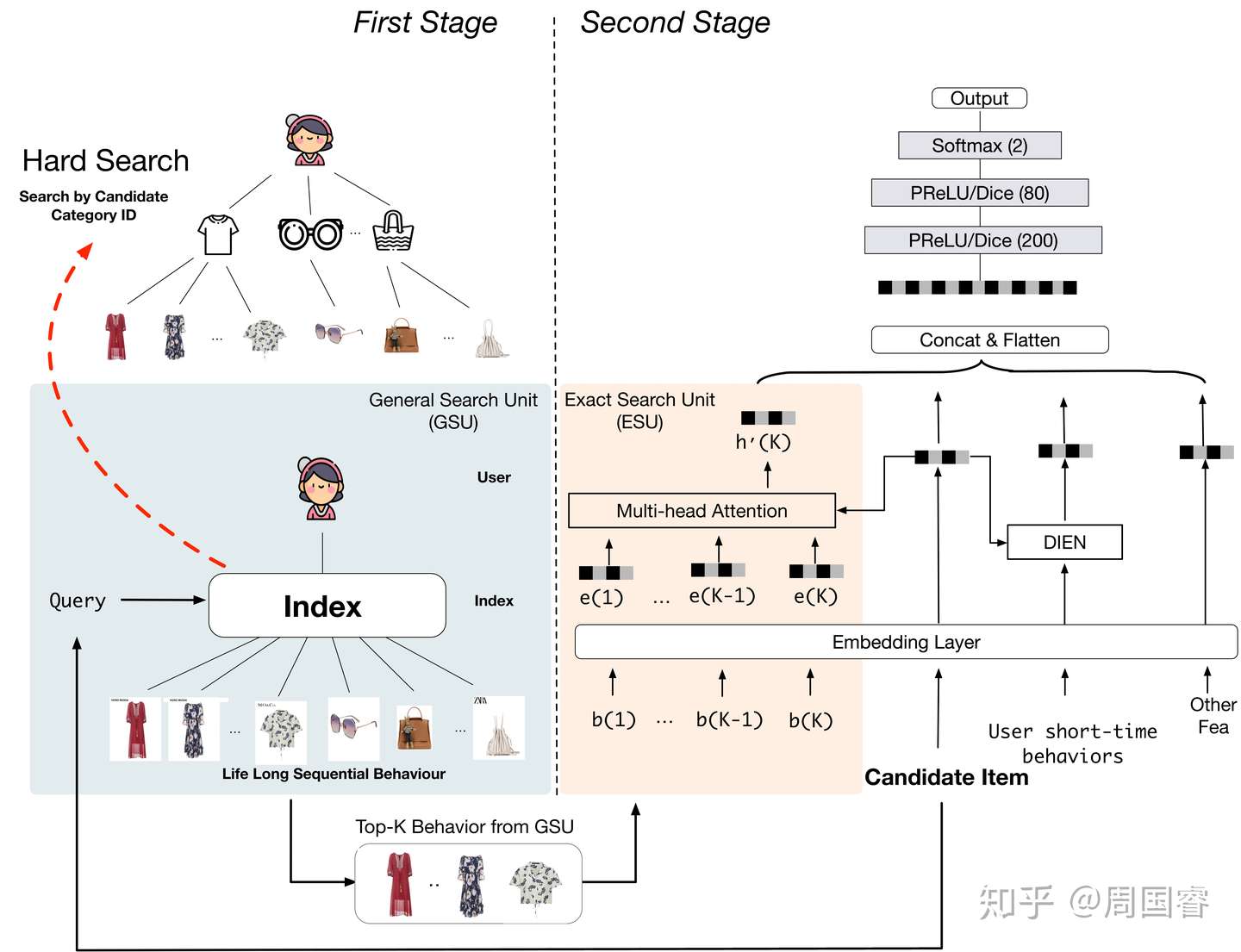
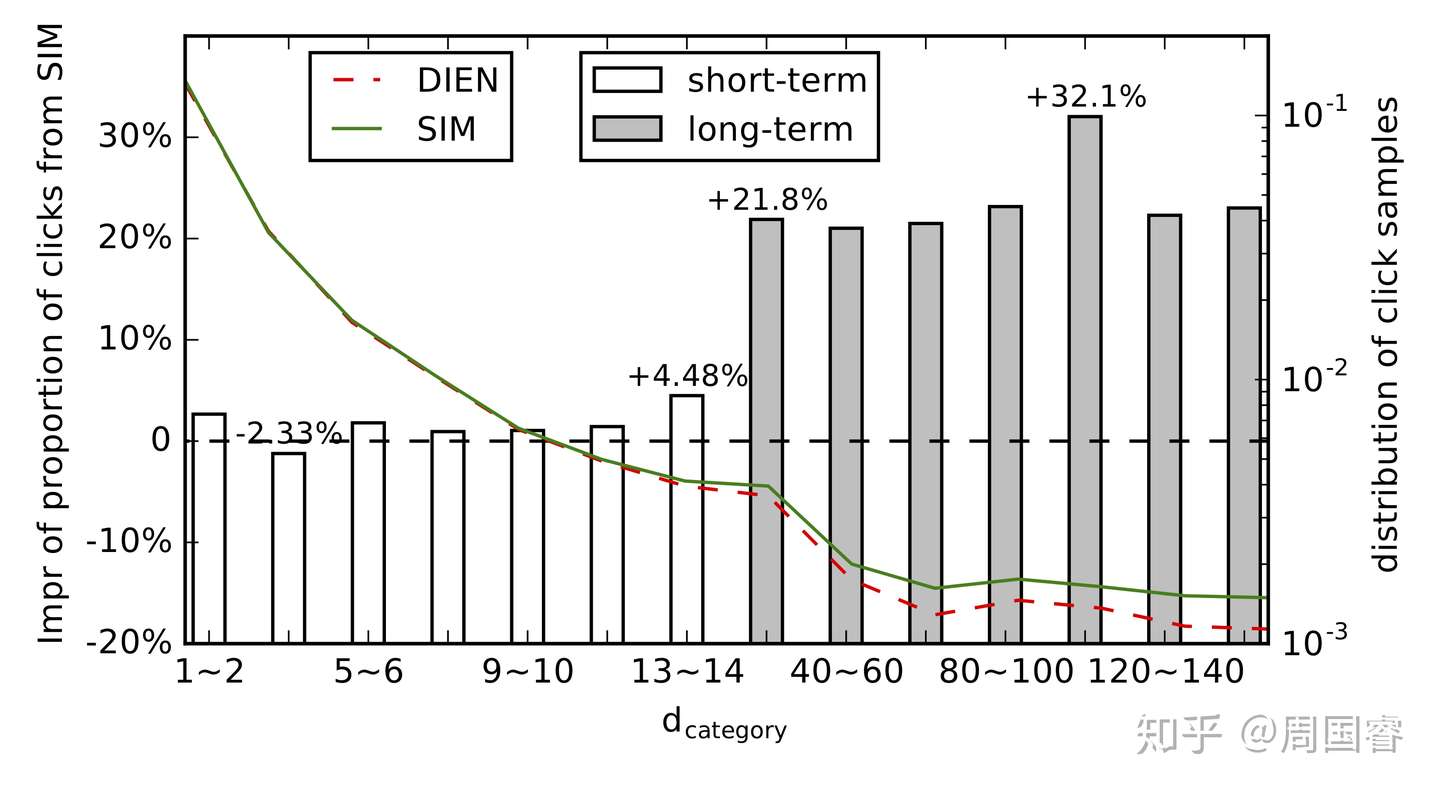
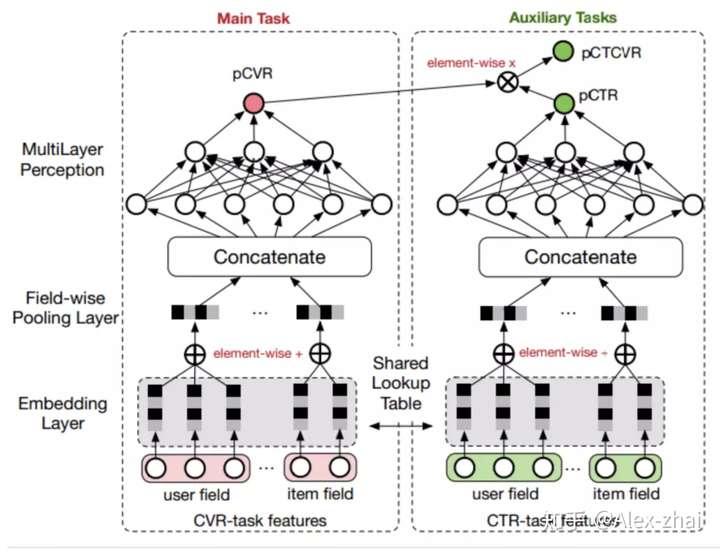
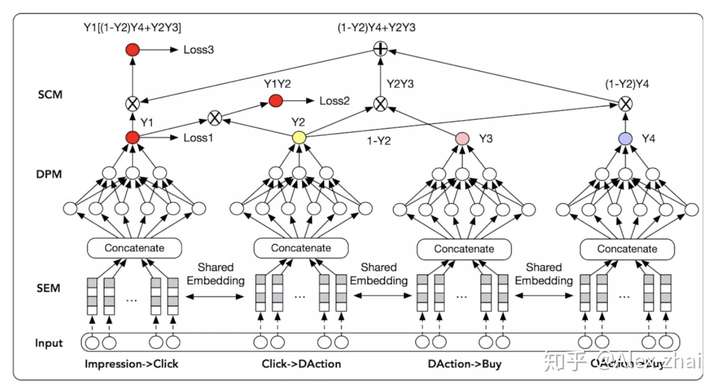
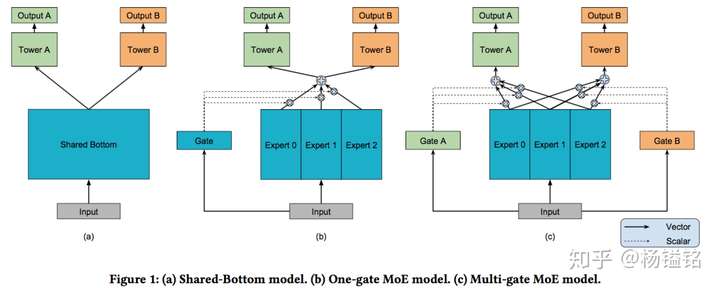
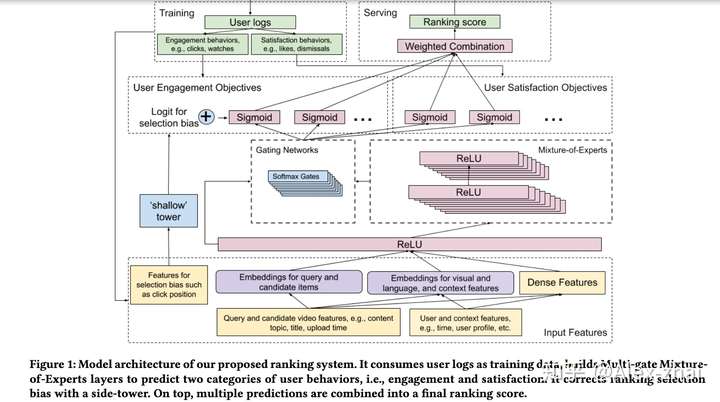
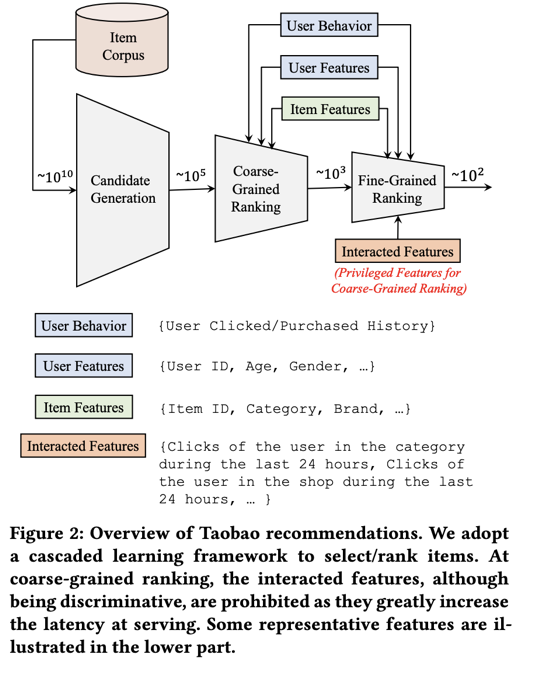
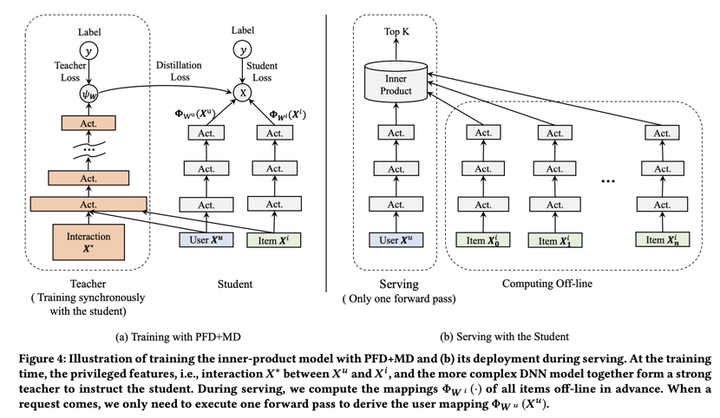
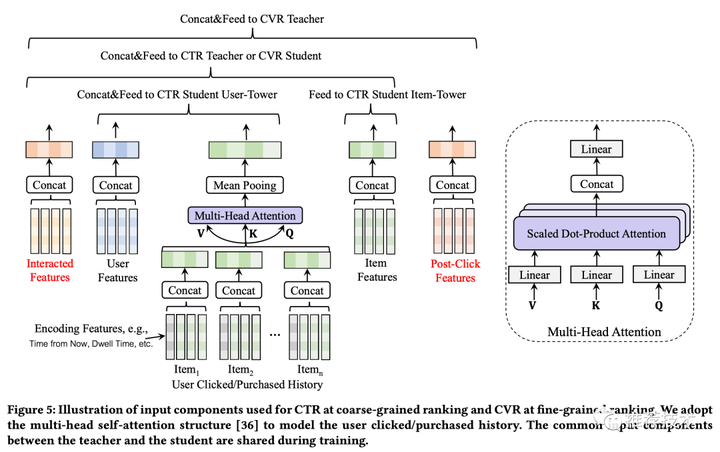
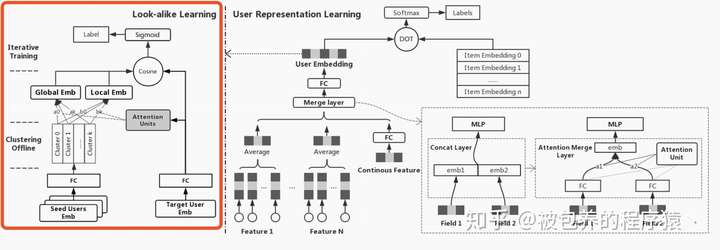
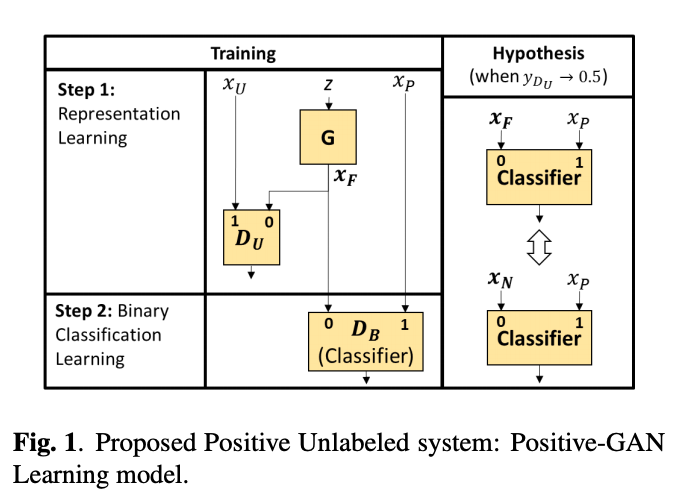
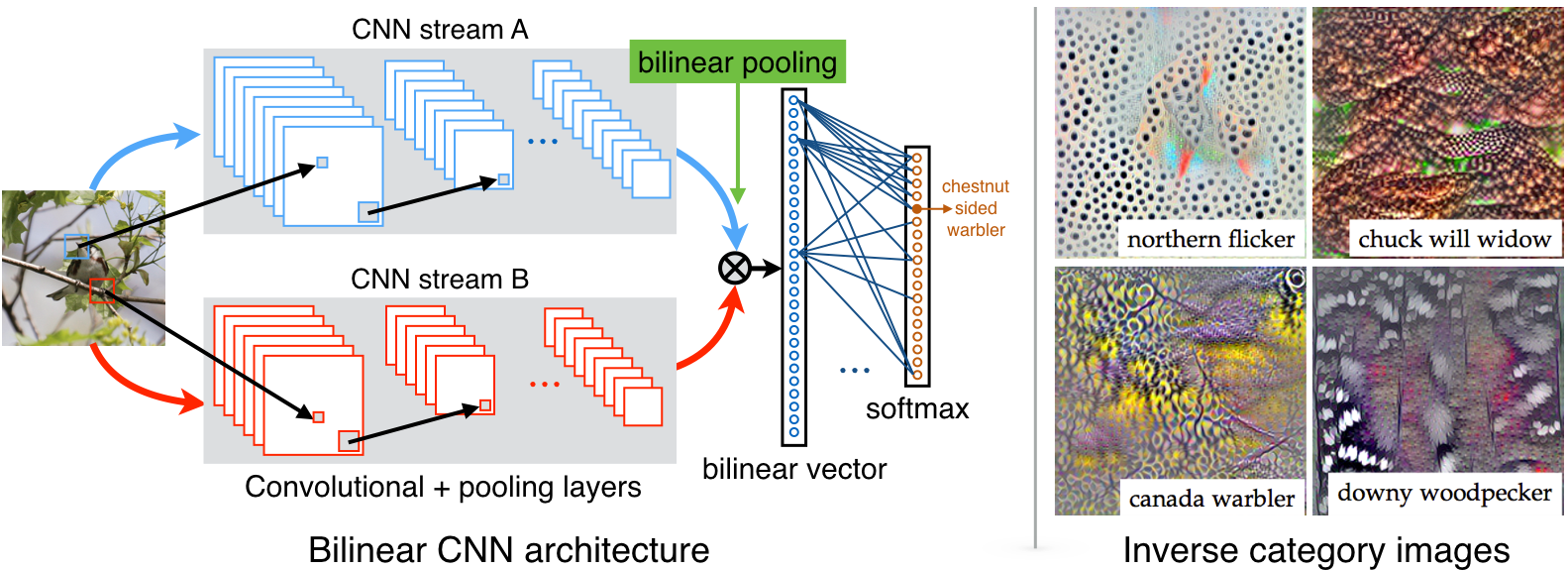
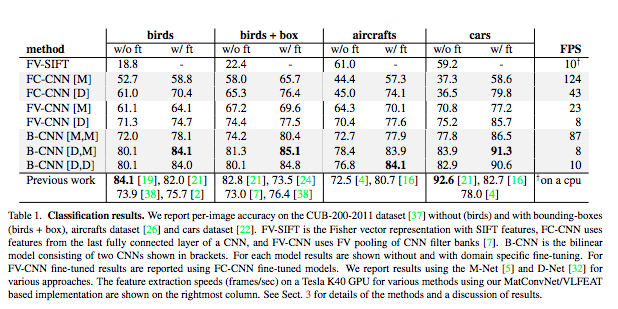
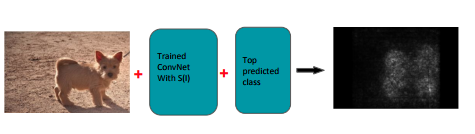
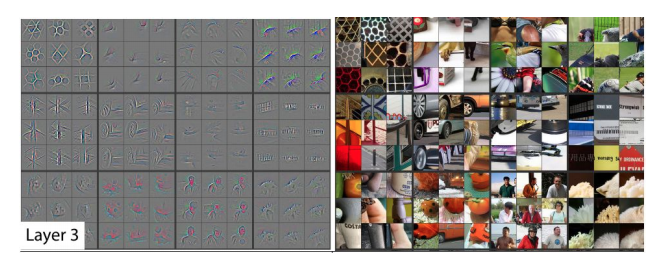
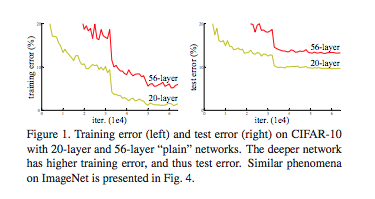
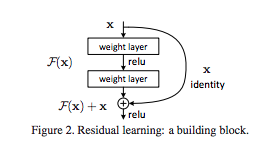
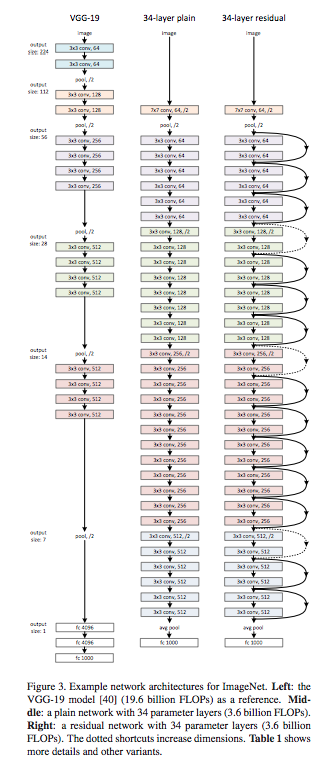
问题

问题：给定用户特征，预估未来n天的付费概率、付费金额

样本：用户特征 $x$ ，标签是未来n天是否付费 $p$ 、付费金额 $y$ 。

数据分布特点：

90% 用户不付费，10% 用户付费
付费用户中，90% 是低付费用户，9% 是高付费用户，1% 是超高付费用户

建模

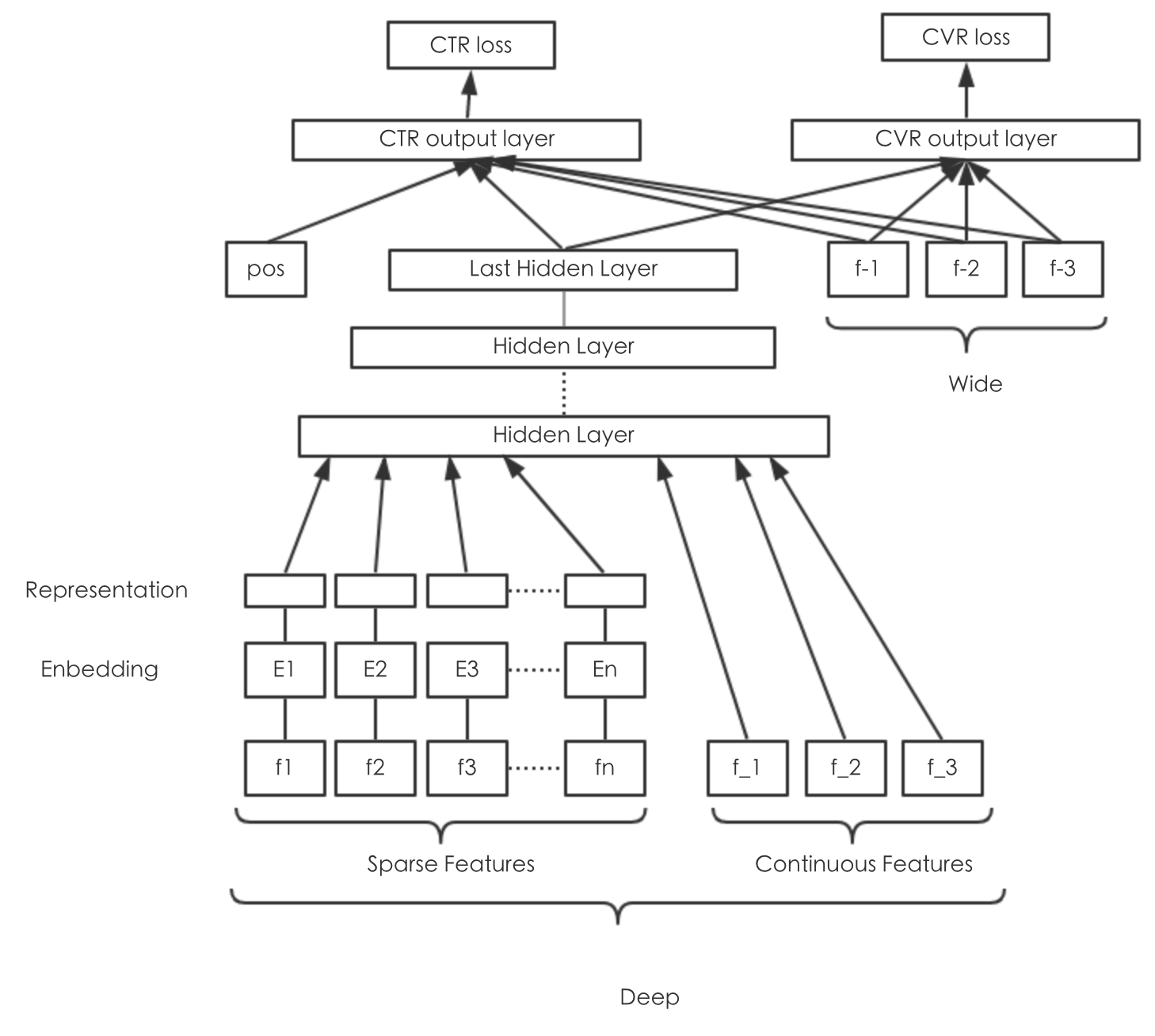
多任务模型，分别预估付费概率和付费金额

$pred\_ltv(x) = pay\_prob(x) \cdot pay\_amount(x)$

付费概率预估损失函数有：

$L_\text{CE}$ 交叉熵损失函数

付费金额预估损失函数有：

$L_\text{MSE}(y,x)=\frac{1}{n}\sum_{i=1}^n (y_i- \hat{y_i}(x_i))^2$
$L_\text{RMSE}(y,x)=\frac{1}{n}\sum_{i=1}^n\sqrt{(y_i- \hat{y_i}(x_i))^2}$
$L_\text{lognormal}(y,x,\mu(x),\sigma(x))=\frac{1}{n}\sum_{i=1}^n \log(y_i\sigma \sqrt{2\pi})+\frac{(\log y_i - \mu)^2}{2\sigma^2}$

其中 $x$ 是用户样本， $y$ 是付费金额； $p,\mu,\sigma$ 分别是付费概率、付费金额均值、付费金额标准差。

MSE Loss 假设拟合误差服从标准正态分布，Loss 是关于均值对称的，对高付费样本，产生较大的 Loss。

ZILN Loss 假设随机变量 LTV 服从对数正态分布，对高付费样本，不会产生较大的 Loss。

考虑样本 LTV 更接近对数正态分布，本文使用 ZILN Loss 建模，获得效果提升。

推导

模型定义

$\begin{aligned} p, \sigma, \mu &= dnn(x_i) \\ pay\_prob(x_i) &= p \\ pay\_amount(x_i) &= \exp(\mu +\frac{\sigma^2}{2})\\ pred\_ltv(x_i) &= pay\_prob(x_i) \cdot pay\_amount(x_i)\\ \end{aligned}$

其中 $p,\sigma,\mu$ 激活函数分别是 sigmoid identity softplus；pay_amount 等于服从对数正态分布的随机变量期望。

其中 $p$ 表示付费概率； $\mu,\sigma$ 表示均值和标准差，是付费金额服从对数正态分布的参数。

损失函数推导

记 $pay\_prob$ 为 $P_1$ ， $pay\_amount$ 为 $P_2$

求参数 $\hat\theta$ 使得极大似然函数最大

$\begin{aligned} \hat\theta & =\arg \max_\theta \text{MLE}(x,y) \\ &= \arg \max_\theta\prod_{x_i,y_i} (1-P_1(x_i))^{\mathbb 1_{y_i=0}}(P_1(x_i)P_2(x_i))^{\mathbb 1_{y_i>0}} \\ &\approx \arg \max_\theta \sum_{x_i,y_i} \mathbb 1_{y_i=0} \log (1-P_1(x_i))+ \mathbb 1_{y_i>0} \log P_1(x_i) + \mathbb 1_{y_i>0} \log P_2(x_i)\\ &\approx \arg \max_\theta \sum_{x_i,y_i} L_\text{CE}(\mathbb 1_{y_i>0};P_1(x_i)) + \mathbb 1_{y_i>0} L_\text{lognormal}(y_i;\mu(x_i), \sigma(x_i)) \end{aligned}$

其中

$\begin{aligned} L_\text{lognormal}(y;\mu(x), \sigma(x))&= -\prod_{x_i,y_i} PDF_\text{lognormal}(y_i;\mu(x_i),\sigma(x_i))\\ &=-\sum_{x_i,x_j} \log(y_i\sigma\sqrt{2\pi}) + \frac{(\log x - \mu)^2}{2\sigma^2} \end{aligned}$

评估

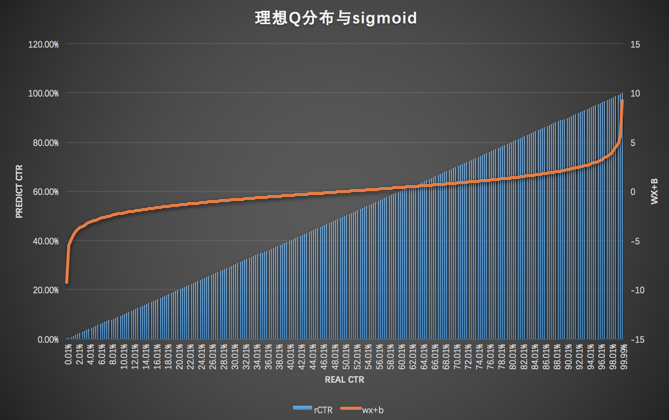
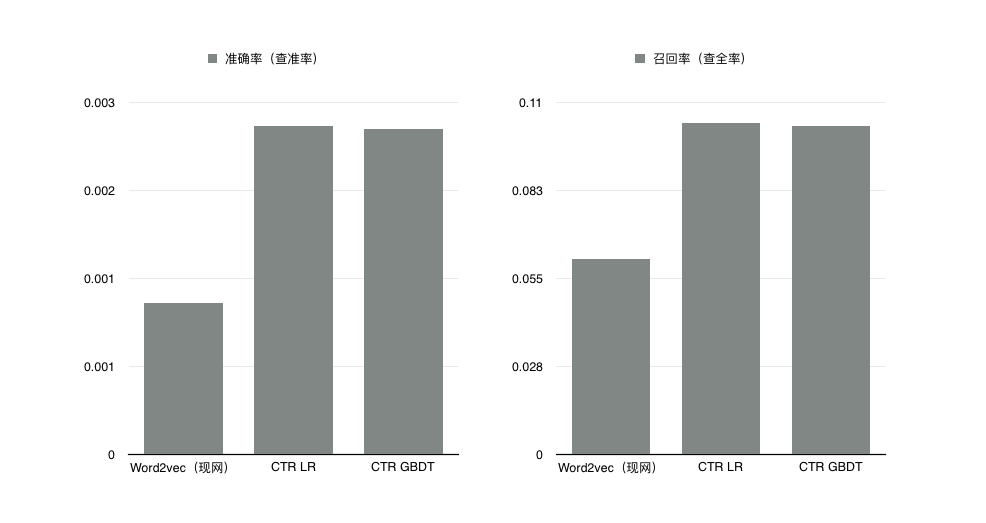
绘制洛伦兹曲线如下图，使用基尼系数（= 预测曲线下面积 / GT 曲线下面积）评估回归模型，使用 AUC 评估分类模型。

使用十分位图评估对不同分数层用户的预测效果：

参考

《A-deep-probabilistic-model-for-customer-lifetime-value-prediction》 PDF 2019 DeepAI Google

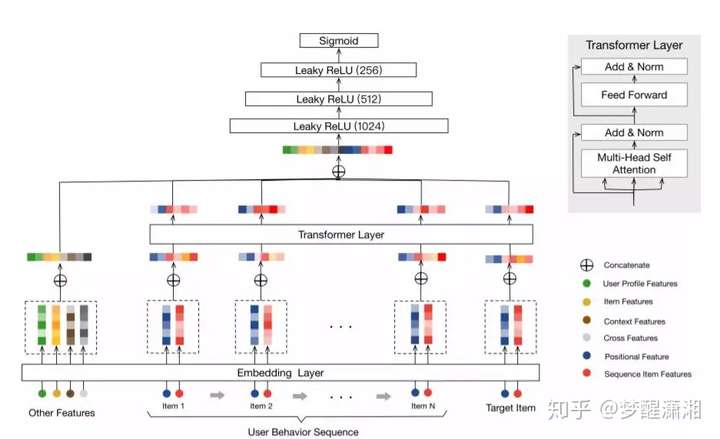
《Behavior Sequence Transformer for E-commerce Recommendation in Alibaba》PDF 2019 阿里

附录

正态分布

概率密度函数 wiki

$PDF_{normal}(x;\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

对数正态分布

概率密度函数 wiki

$PDF_{lognormal}(x;\mu,\sigma)=\frac{1}{x\sigma\sqrt{2\pi}} e^{-(\ln x - \mu)^2 / 2\sigma^2}$

期望 $E(X) = e^{\mu + \sigma^2/2}$

方差 $var(X)=(e^{\sigma^2} - 1) e^{2\mu + \sigma^2}$

如果随机变量 $X$ 的对数服从正态分布，则这个随机变量服从对数正态分布。

如果 $Y$ 是正态分布的随机变量，则 $\exp(Y)$ 为对数正态分布。

如果 $X$ 是对数正态分布，则 $\ln X$ 为正态分布。

如果一个变量可以看作是许多很小独立因子的乘积，则这个变量可以看作是对数正态分布。一个典型的例子是股票投资的长期收益率，它可以看作是每天收益率的乘积。

中心极限定理

大量统计独立的随机变量的平均值的分布趋于正态分布。

LogNormal Loss 推导

假设随机变量 $y$ 符合 Log Normal 分布，其概率密度函数为

$PDF_{LogNormal}(x;\mu,\sigma) = \frac{1}{x \sigma\sqrt{2\pi}}e^{-(\ln x-\mu)^2/2\sigma}$

从对数最大似然函数可以推导出 LogNormal Loss

$LL_{lognormal}(y;\mu,\sigma) =\prod_{i=0}^m PDF_{LogNormal}(x=y_i;\mu,\sigma)= \sum_{i=0}^m \log(y_i\sigma\sqrt{2\pi}) + \frac{(\ln y_i - \mu)^2}{2\sigma^2}$

TF 实现，其中 loc scale label 对应 $\mu,\sigma,y$ ：

1	regression_loss = -tf.keras.backend.mean(tfd.LogNormal(loc=loc, scale=scale).log_prob(labels),axis=-1)

MSE Loss 推导

假设目标与输入变量存在如下关系，且误差服从标准正态分布

$y_i = h_\theta(x_i)+\epsilon_i$

$\epsilon_i\in N(\mu=0,\sigma^2=1)$

正态分布概率密度函数

$PDF_{Norm}(x;\mu,\sigma)=\frac{1}{\sqrt{2\pi}}\exp{(-\frac{1}{2}(\frac{x-\mu}{\sigma}})^2)$

误差概率密度函数

$p(\epsilon_i;\mu=0,\sigma=1)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{\epsilon_i^2}{2})$

给定 $x_i$ 模型输出 $y_i$ 的概率 $p$ 为

$p(y_i|x_i)=\frac{1}{\sqrt{2\pi}}\exp{(-\frac{(y_i - h_\theta(x_i))^2}{2})}$

从对数最大似然函数可推导出 MSE Loss

$LL_{MSE}=\log\prod_{i=0}^{m} p(y_i|x_i;\theta)=m\log\frac{1}{\sqrt{2\pi}}-\frac{1}{2}\sum_{i=1}^m (y_i - h_\theta(x_i))^2$

MAE Loss 推导

假设目标与输入变量存在如下关系，且误差服从拉普拉斯分布

$y_i = h_\theta(x_i)+\epsilon_i$

$\epsilon_i\in L(\mu=0,b=1)$

拉普拉斯概率密度函数

$PDF_{Laplace}(x;\mu,b)=\frac{1}{2b}\exp(-\frac{|x-\mu|}{b})$

误差概率密度函数

$p(\epsilon_i;\mu=0,b=1)=\frac{1}{2}\exp(-|\epsilon|)$

给定 $x_i$ 模型输出 $y_i$ 的概率 $p$ 为

$p(y_i|x_i)=\frac{1}{\sqrt{2\pi}}\exp{(-\frac{|y_i - h_\theta(x_i)|}{2})}$

从对数最大似然函数可推导出 MSE Loss

$LL_{MAE}=\log\prod_{i=0}^{m} p(y_i|x_i;\theta)=m\log\frac{1}{\sqrt{2\pi}}-\frac{1}{2}\sum_{i=1}^m |y_i - h_\theta(x_i)|$

Huber Loss

将 MSE 与 MAE 结合起来，[-1,1] 用 MSE 平滑，其余区间用 MAE。

对比

MSE 比 MAE 收敛更快

MAE 比 MSE 对异常点更加鲁棒

deep-nlp-models

Posted on 2020-08-07

https://zhuanlan.zhihu.com/p/56176647

https://tech.meituan.com/2019/11/14/nlp-bert-practice.html

独热编码语言模型

要点：用 one-hot 向量表示词，用 Bag-of-Words multi-hot 向量表示句子。

问题：维度灾难，语义鸿沟

矩阵分解语言模型

基于SVD

对共现矩阵（Window based Co-occurrence Matrix / Word-Doc Matrix）A 分解

$A=U\Sigma V^T$

$A\in\mathbb R^{m*n}, U\in\mathbb R^{m*m}, \Sigma \in\mathbb R^{m*n}, V\in\mathbb R^{n*n}$

问题：矩阵稀疏，计算复杂度高，高频词影响结果，一词多意问题。

统计语言模型

对于语言序列 $w_1,w_2,...,w_n$ ，语言模型用于计算序列出现的概率 $P(w_1,w_2,...,w_n)$

N-gram

假设第n个词出现仅与n-1个词有关（马尔可夫假设）。

当 n = 2 有

$P(w_1,w_2,...,w_n) = P(w_1|start) P(w_2|w1) ... P(w_n|w_{n-1})$

浅层神经网络语言模型

NNLM

《A Neural Probabilistic Language Model》PDF Bengio 2003 提出，用 NN 代替 N-gram 基于统计预估模型的方法。

用前 n-1 个词去预测第n个词的概率，通过 softmax 输出维度 d 的向量，表示每个词出现的概率。

输入 n-1 个词作 emb lookup 后拼接（x），输入 tanh，加上残差

$y= b+Wx+U\tanh(d+Hx)$

最后用 softmax 对输出概率作归一化

P(w_t |w_{t−1},···w_{t−n+1}) = \frac{e^{y_{w_t}}}{\sum_i e^{y_i}} .

其中 tanh -> softmax 最为耗时，后续算法基于 NNLM 改进。

Wordvec

要点：学习单词的 context 相似性特征；CBOW 目标最大化通过上下文词预测当前词的生成概率，Skip-Gram 目标最大化通过当前词预测上下文词的生成概率。

问题：无法学习句法、语义特征

SkipGram

目标函数

$J=\frac{1}{T}\sum_{t=1}^{T}\sum_{-m \le j\le m,j\ne0} \log p(w_{t+j}|w_t)$

其中条件概率为

$p(w_{t+j}|w_t) = \frac{\exp(u_{w_{t+j}}^T v_{w_t})}{\sum_{i=1}^W \exp(u_{w_i}^T v_{w_t})}$

其中， $T$ 表示数据机中样本窗口数，m 表示样本窗口大小，W 表示词表大小。

因为对同一样本窗口，CBOW 模型计算一次梯度， SkipGram 计算窗口大小次数的梯度。SkipGram 对低频词到表示通常优于 CBOW，而速度慢于 CBOW。论文中引入负采样和层次Softmax来提高效率。

https://zhuanlan.zhihu.com/p/54578457

https://mp.weixin.qq.com/s/FwaCMCfLPpQ6YqbSwZeNxA

对比	ELMo	GPT	BERT
输入层	词序列	词序列	词序列+句子向量+位置向量
网络结构	双向 LSTM	Trans 单向编码器	Trans 双向编码器
预训练任务	双向语言模型	单向语言模型	掩码语言模型+下一句预测
融合方式	特征融合	参数微调+辅助任务	参数微调

自回归语言模型

Autogressive LM，通过上文预测下一个字，或者反之。

Seq2Seq

论文：

《Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation》PDF Bengio Google 2014，RNN ENcoder-Decoder

《Sequence to Sequence Learning with Neural Networks》PDF Quoc V. Le Google 2014，LSTM ENcoder-Decoder

要点：

实现：https://google.github.io/seq2seq/ https://github.com/google/seq2seq

ConvS2S

论文：《Convolutional Sequence to Sequence Learning》PDF FAIR 2017

参考：https://zhuanlan.zhihu.com/p/60524073

Transformer

论文：《Attention is All You Need》PDF 2017

要点：与 LSTM GRU 等循环网络相比，通过 Self-Attention 机制能够高效学习长距离 token emb 交互，并行性好，计算复杂度低。BLEU 41 SNLI 89.3

优点：

Scaled Dot-Product Self-Attention

$\begin{aligned} Attention(Q,K,V) &= Softmax(QK^T/\sqrt{d_k})V \\ \end{aligned}$

Multi-head Attention

$\begin{aligned} MultiHead(Q,K,V) &= Concat(head_1,head_2,...,head_n)W^O \\ head_i &= Attention(QW_i^Q,KW_i^K,VW_i^V,) \end{aligned}$

Point-wise Feed-Forward Networks

$FFN(x)=\max(0,xW_1+b_1)W_2+b_2$

Positional Encoding

硬编码：sinosoidal function，在偶数位置正弦编码，在奇数位置余弦编码。
软编码：learnable embedding lookup

效果相近，前者更容易外推到更长序列。

Optimizer

Adam with

$learning\_rate=d_{model}^{-0.5} \cdot \min (step\_num^{-0.5}, step\_num \cdot warmup\_steps^{-1.5})$

ELMo

Embedding from Language Models

论文：《Deep contextualized word representations》 PDF 2018

要点：两层双向 LSTM 学习句法和语义特征，解决一词多义问题。SQuAD 85.8 SNLI 88.0

比如 I like apple [product]，其中 apple 根据上下文调整 emb

与之前工作不同的是，该模型不仅去学习单词特征，还有句法特征与语义特征。后两者的特征是来自LSTM的隐含输出向量。这里的模型目标是预测对应位置的下一个单词（也就是T1的向量应该预测出E2的单词）。

模型训练完，我们就可以得到单词，句法以及语义特征。也就是在一个句子中每一个单词将会对应三个向量，然后三者共同构建成下游任务的输入。比如下游任务就是一个对话系统，整个流程如下图所示。

总结就是ELMo模型是通过语言模型任务得到句子中的单词的向量，这个向量是结合左向右向的信息，但是仅仅是拼接的实现。

GPT

论文：《Improving Language Understanding by Generative Pre-Training》PDF 2018

要点：引入单向 transformer 替换 LSTM，模型的任务有txt prediction与Task classifier。需要注意的是这里的transformer只有decode部分。

得到预训练的模型，然后在这样的模型后面再次接上下游任务。与ELMo只提供向量不同，这里预训练的模型一同提供给下游的任务。这里模型的向量是可以随着新的下游任务发生微小的调整，也就是fine-tune。

自编码语言模型

Autoencoder LM，区别于自回归 LM，根据上下文预测中间词。

如 BERT 输入随机 mask 一部分词对其预测，类似 Denoising Autoencoder（输入噪音图片，输出去噪图片）。

优点是可以利用上下文进行预测，缺点输入侧引入 Mask 标记，导致预训练阶段和 Fine-tuning 阶段（无 Mask 标记）不一致问题。BERT 这个方法缓解这个问题：对 15% 需要 Mask 词汇，80% 概率用 Mask、10% 用其他词替换、10% 维持不替换。

BERT

论文：《BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding》PDF 2019

要点：Transformer 双向编码器 + 掩码语言模型；先用两个任务预训练模型，再接入任务塔进行 fine-tune。

数据：BooksCorpus、Wiki，大小13G。

意义：

真正双向多层语言模型，词语义建模+上下文同时建模
显式对句子关系建模

预训练：

MLM, Masked Language Model：对输入词，构建完形填空任务。改善以往模型自左向右，或浅层拼接自左向右、自右向左模型的上下文学习能力
NSP, Next Sentence Prediction：判断两句时候相连的二分类问题，用于 QA 任务；最近研究发现，去掉 NSP 影响不大。

网络结构：全连的网络结构（与 GPT 比较）。

输入向量：词向量（ $E_{word}$ / $E_{CLS}$ / $E_{SEP}$ ），段落向量（segment embedding, $E_A$ / $E_B$ ）与位置向量（position embedding, $E_i$ ），都需要模型学习。

输入的格式：增加了 $[CLS],[SEP]$ ，为了能同时表达 <单句> 和 <问题句, 答案句="">，给下游各种任务。

MT-BERT

文章：https://tech.meituan.com/2019/11/14/nlp-bert-practice.html

要点：

模型轻量化 & 分布式训练 & 推导加速
领域自适应：在 Google 中文BERT模型上加入领域数据
知识融入：Knowledge-aware Masking，融入实体知识，避免如 “宫保鸡丁”和“宫保鸡丁酱料” 距离相近的问题
单句分类——细粒度情感分析，Share Layers (多路并行的Attention) + Task-specific Layers，对文本在各个属性上的情感倾向进行分类预测（环境、服务、口味多分类）
介绍其他任务应用，如推荐理由场景化分类、Query意图分类

RoBERTa

论文：《RoBERTa: A Robustly optimized BERT approach》PDF ACL19

要点：更多的数据，采取更精妙的训练技巧，训练更久一些

效果：在 GLUE / RACE / SQuAD 取得 SOTA

ALBERT

论文：《ALBERT: A Lite BERT for Self-supervised Learning of Language Representations》PDF ICLR20

要点：压缩 BERT，从 100M 到 12M

优化：

Factorized embedding parameterization
Cross-layer parameter sharing
Inter-sentence coherence loss

《美团BERT的探索和实践》URL 模型裁剪

排列语言模型

Permutation LM，基于自回归 LM，通过 Attention Mask 实现双流自注意力，融入双向语言模型。

XLNet

论文：《XLNet: Generalized Autoregressive Pretraining for Language Understanding》PDF Google 2019

参考：《XLNet:运行机制及和Bert的异同比较》URL

数据：BooksCorpus、Wiki、Giga5、CluWeb、CommonCrawl，大小16G、19G、78G。

要点：

解决自回归 LM 如 ELMO 的问题：只编码单向语意
解决自编码 LM 如 BERT 的问题： (a) 预测 Mask 词之间互相独立的假设 (b) 训练使用 Mask 预测中不用造成的误差
提出排列 LM，通过 Attention Mask 随机排列输入句子、预测某个位置的词。

T5

论文：《Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer》PDF Google 2020

介绍：https://ai.googleblog.com/2020/02/exploring-transfer-learning-with-t5.html

要点：提出 T5 框架，涵盖所有 NLP 任务到单一 text-to-text 模型。

附录

NLP可以分为自然语言理解（NLU）和自然语言生成（NLG）。

NLU 较流行的是 GLUE(General Language Understanding Evaluation) ，集合了九项NLU的任务：

CoLA(The Corpus of Linguistic Acceptability):纽约大学发布的有关语法的数据集，该任务主要是对一个给定句子，判定其是否语法正确，因此CoLA属于单个句子的文本二分类任务；
SST(The Stanford Sentiment Treebank)，是斯坦福大学发布的一个情感分析数据集，主要针对电影评论来做情感分类，因此SST属于单个句子的文本分类任务（其中SST-2是二分类，SST-5是五分类，SST-5的情感极性区分的更细致）；
MRPC(Microsoft Research Paraphrase Corpus)，由微软发布，判断两个给定句子，是否具有相同的语义，属于句子对的文本二分类任务；
STS-B(Semantic Textual Similarity Benchmark)，主要是来自于历年SemEval中的一个任务（同时该数据集也包含在了SentEval），具体来说是用1到5的分数来表征两个句子的语义相似性，本质上是一个回归问题，但依然可以用分类的方法做，因此可以归类为句子对的文本五分类任务；
QQP(Quora Question Pairs)，是由Quora发布的两个句子是否语义一致的数据集，属于句子对的文本二分类任务；
MNLI(Multi-Genre Natural Language Inference)，同样由纽约大学发布，是一个文本蕴含的任务，在给定前提（Premise）下，需要判断假设（Hypothesis）是否成立，其中因为MNLI特点是集合了许多不同领域风格的文本，因此又分为matched和mismatched两个版本的MNLI数据集，前者指训练集和测试集的数据来源一致，而后者指来源不一致。该任务属于句子对的文本三分类问题。
QNLI（Question Natural Language Inference)，其前身是SQuAD 1.0数据集，给定一个问句，需要判断给定文本中是否包含该问句的正确答案。属于句子对的文本二分类任务；
RTE(Recognizing Textual Entailment)，和MNLI类似，也是一个文本蕴含任务，不同的是MNLI是三分类，RTE只需要判断两个句子是否能够推断或对齐，属于句子对的文本二分类任务；
WNLI(Winograd Natural Language Inference)，也是一个文本蕴含任务，不过似乎GLUE上这个数据集还有些问题；

NLG 常见的数据集：

BLEU（机器翻译）《BLEU: a Method for Automatic Evaluation of Machine Translation》PDF IBM 2002
ROUGE（自动摘要）、Rouge-N、Rouge-L、Rouge-W、Rouge-S
METEOR（机器翻译、自动文摘），《METEOR: An automatic metric for mt evaluation with improved correlation with human judgments》PDF CMU 2005
CIDEr（图像）《CIDEr: Consensus-Based Image Description Evaluation》PDF CVPR 2015

延迟反馈问题

Posted on 2020-07-14

常见于在线 pCTR pCVR 预估任务，挑战：窗口期正样本少；窗口期负样本会延迟转化；时间窗口过大影响在线指标。

在线学习算法篇(一) 样本延迟反馈 KM

CVR 预估中的转化延迟反馈问题概述知乎

Importance Sampling

是通过从一个数据分布的采样，估算另一个数据分布的采样的方法。

关于模型 $f_\theta$ 和数据分布 $p$ ，交叉熵的定义是

$L(\theta)=-\mathbb{E}_p[\log f_\theta(y|x)]=-\sum_{x,y}p(x,y)\log f_\theta(y|x)$

在线采样有偏导致数据分布为 $b$ ，而我们无法从数据分布 $p$ 中采样，通过恰当的 weighting scheme 我们能获得无偏估计：

$\mathbb{E}_p[\log f_\theta(y|x)]=\mathbb{E}_b[\frac{p(x,y)}{b(x,y)} \log f_\theta(y|x)] = \frac{1}{N} \sum_n w(x_n,y_n) \log f_\theta(y_n|x_n)$

其中 $w(x,y)= \frac{p(x,y)}{b(x,y)}$ 是 importance weight

此方法的挑战，是需要对 $w$ 作出合理估计。

此方法广泛用于反事实分析（counterfactual analysis）：微软 Bottou et. al. 在《Counterfactual reasoning and learning systems: The example of computational advertising JMLR13》 PDF 讨论了如何在计算广告应用此方法估算 counterfactual expectation。

例子：https://zhuanlan.zhihu.com/p/41217212

Inverse Propensity Weighting

《Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies》PDF

在临床药理研究中，通常治疗组（Y = 1）的指派不是随机的，建模倾向分数（propensity score） $p(x)=P(Y=1|X=x)$ ，即某个样本 x 被指派为治疗组的概率；然后通过逆倾向分数对样本加权。

在 pCTR 问题中，Y=1 表示点击样本。

此方法的挑战，是需要对倾向分数单独建模。

例子：https://en.wikipedia.org/wiki/Inverse_probability_weighting

Delayed Bandits

《Markov decision processes with delays and asynchronous cost collection》

《Stochastic Bandit Models for Delayed Conversions》

《Learning and planning in environments with delayed feedback》

kdd2020

Posted on 2020-07-06

《Privileged Features Distillation at Taobao Recommendations KDD20 Ali》PDF

淘系推荐提出 PFD 方法，提升 CVR 准确率：在离线环境下，同时训练两个模型：一个学生模型和一个教师模型。其中教师模型额外利用了秘密特征（比如 CVR 任务中，在商详页点击评论次数），则准确率更高。将教师模型蒸馏出来的知识传递给学生模型，辅助其训练，提升学生的准确率。线上服务时，只用学生模型进行部署，由于输入中不依赖秘密特征，则保证了线上线下特征的一致性。

主要参考《UNIFYING DISTILLATION AND PRIVILEGED INFORMATION ICLR16》PDF

knowledge-distillation

Posted on 2020-05-26

《Distilling the Knowledge in a Neural Network Hinton15》PDF

用简单的 student 网络的 logit 学习复杂的 teacher 网络的 logit。

《Ranking Distillation: Learning Compact Ranking Models With High Performance for Recommender System》

《知识蒸馏在推荐系统的应用》知乎

《推荐系统技术演进趋势：从召回到排序再到重排》知乎

graph-nerual-network

Posted on 2020-05-08

GCN

Graph Convolutional Network

Transductive / Inductive Task

transductive 转导任务：训练阶段与测试阶段都基于同样的图结构，如 pubmed cora 数据集。

常见算法：LabelPropagation SemiEmb ManiReg DeepWalk

Inductive 归纳任务：训练阶段与测试阶段都基于不同的图结构，可对未知测试点进行预测，如 protein-protein interaction 数据集

常见算法：GAT，GraphSAGE-GCN/LSTM/mean，

GraphSage

Spatial Domain

基于空域卷积的方法直接将卷积操作定义在每个结点的连接关系上，它跟传统的卷积神经网络中的卷积更相似一些。在这个类别中比较有代表性的方法有 MPNN GraphSage MoNet

Spectral Domain

这就是谱域图卷积网络的理论基础了。这种思路就是希望借助图谱的理论来实现拓扑图上的卷积操作。从整个研究的时间进程来看：首先研究 GSP（graph signal processing）的学者定义了 graph 上的 Fourier Transformation，进而定义了 graph 上的 convolution，最后与深度学习结合提出了 Graph Convolutional Network。

GCN

谱域，inductive 任务，拉普拉斯矩阵

GraphSAGE

《Inductive Representation Learning on Large Graphs NIPS17》 PDF

空域，inductive 任务

https://zhuanlan.zhihu.com/p/62750137

预测任务，输出：给定节点的标签，输入：采样1、2条节点的 embedding 进行聚合

PinSage

《Graph Convolutional Neural Networks for Web-Scale Recommender Systems》PDF

https://zhuanlan.zhihu.com/p/63214411

EGES

《Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba》KDD18

可以根据用户的历史行为来构建商品图（如上图的a和b，根据用户的一些点击记录，依照连续点击应该存在关系，可以构造出如b一样的item graph），并学习图中所有商品的嵌入（如图c的带权随机游走采样，用deepwalk思想基于skip-gram训练embedding）。这一步就是作者描述的Base Graph Embedding（BGE）。

为了减轻稀疏性和冷启动问题，将边信息合并到图嵌入框架中。即增加商品的属性，如品牌，价格等。然后就升级成了Graph Embedding with Side information (GES)，并且对不同的side Information加权得到Enhanced Graph Embedding with Side information (EGES)。

GraphTR

《Graph Neural Network for Tag Ranking in Tag-enhanced Video Recommendation CIKM20》PDF

https://mp.weixin.qq.com/s/0Tb5t9K2V-RYb12UKL1cXg

https://github.com/lqfarmer/GraphTR

微信

GAT

空域，inductive / transductive 任务

GAT 注意力系数，有向

https://zhuanlan.zhihu.com/p/81350196

https://www.youtube.com/watch?v=6hbWpbi0Z24

贝叶斯学派 v.s. 频率学派

Posted on 2020-02-25

给定训练数据集 $X$ 和参数 $\theta$

其中 $X=(x_0, x_1, …, x_n), x \sim^{i.i.d.} P(X|\theta) $

为简化记 $P(X|\theta) = \prod_{i=1}^{n} P(x_i|\theta)$

频率派

假设

认为 $\theta$ 是未知常量， $X$ 是随机变量。

参数估计

MLE 极大似然估计：似然函数连乘最大化

$\theta_{MLE}= \arg \max_\theta \log P(X|\theta)$

套路

统计机器学习模型：概率模型、判别模型
问题定义和损失函数设计
求解优化问题

举例

假设扔硬币观察正反面变量 $X$ 服从二项分布 $P(X=1|\theta)=\theta,P(X=0|\theta)=1-\theta$

实验 44581 次，观测到正面 39640 次正面，用 MLE 极大似然估计求解 $\theta$

$\theta^*=\arg\max_\theta \theta^{39640}(1-\theta)^{4941} = 0.8894$

与古典概率学求解结果相同，但小样本可能导致预估偏差大，可尝试贝叶斯派方法

贝叶斯派

假设

认为 \theta～P(\theta) 是随机变量， $X$ 是随机变量

后验概率 = (似然度 * 先验概率)/标准化常量

$P(\theta|X)=\frac{P(X|\theta)P(\theta)}{P(X)} \propto P(X|\theta)P(\theta)$

其中 $P(X)$ 可写为累加或积分形式 $\int_\theta P(X|\theta)P(\theta) d\theta$

其中 $P(\theta|X)$ 是后验概率， $P(X|\theta)$ 是似然（likelihood）， $P(\theta)$ 是先验概率、对参数默认分布假设。

参数估计

MAP 最大后验概率估计：寻找最优 $\theta$ 使得后验概率最大

$\theta_{MAP} = \arg\max_\theta P(\theta|X)=\arg\max_\theta P(X|\theta) P(\theta)$

贝叶斯预计：估计 $\theta$ 关于 $X$ 的概率分布，较难求解

P(\theta|X) = \frac{P(X|\theta)P(\theta)}{\int_\theta P(X|\theta)P(\theta) d\theta}

贝叶斯预测：通过 $P(\theta|X)$ 求 x 的概率分布

$P(\tilde x|X) = \int P(\tilde x,\theta|X)d\theta = \int P(\tilde x|\theta)P(\theta|X)d\theta$

套路

概率图模型：HMM / CRF
求解积分问题：EM / MCMC / 蒙特卡洛模拟等方法

区别

以抛硬币正面朝上的概率为例：

对随机变量如何看待：

频率派：随机变量是固定值，通过不断重复实验逼近
贝叶斯派：开始变量服从某一分布，通过实验观测结果，对参数估计产生变化。

适合场景：

频率排：先验知识弱，样本多
贝叶斯派：先验知识强，样本少

例子

给定数据集

$D=\{(x_1, y_1), (x_2, y_2), ...,(x_n, y_n)\}$

考虑线性回归模型

$y=\theta^T x + \epsilon$

先说结论：

模型参数服从【高斯】分布，贝叶斯派 MAP 估计结果和频率派 MLE +【L1】正则估计结果一致
模型参数服从【拉普拉斯】分布，贝叶斯派 MAP 估计结果和频率派 MLE +【L2】正则估计结果一致

再做推导：

假设随机变量服从分布

$\epsilon \sim N(0, \sigma^2), y \sim N(\theta^Tx, \sigma^2)$

频率派优化目标函数和 L2 正则，得到参数解：

\begin{align} \hat{\theta}_{MLE} &= \arg \min_\theta \prod_{i=1}^{n} P(y_i|x_i;\theta) + \lambda ||\theta||^2 \\ &= \arg \min_\theta \sum_{i=1}^{n} \log P(y_i|x_i;\theta) + \lambda ||\theta||^2 \\ &= \arg \min_\theta \sum_{i=1}^{n} \big(\log \frac{1}{\sqrt{2\pi}\sigma} + \log \exp{(-\frac{(y_i - \theta^Tx)^2}{2\sigma^2})}\big) + \lambda ||\theta||^2\\ &\approx \arg \min_\theta \sum_{i=1}^{n} (y_i - \theta^T x_i)^2 + \lambda ||\theta||^2 \end{align}

其中 $P(y_i|x_i;\theta)=PDF_{norm\_dist}(y_i;\mu=\theta^Tx_i,\sigma)=\frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(y_i -\mu)^2}{2\sigma^2}}$

贝叶斯派假设模型参数符合高斯分布

$\theta \sim N(0, \sigma_0^2)$

$P(\theta|y)=\frac{P(y|\theta)P(\theta)}{p(y)}$

优化目标函数

\begin{align} \hat\theta_{MAP}&=\arg\max_\theta P(\theta|y)=\arg\max_\theta P(y|\theta)P(\theta)\\ &=\arg\max_\theta \frac{1}{\sqrt{2\pi}\sigma} \exp{(-\frac{(y-\theta^Tx)^2}{2\sigma^2})} \frac{1}{\sqrt{2\pi}\sigma_0}\exp{(-\frac{||\theta||^2}{2\sigma_0^2}} )\\ &\approx \arg \min_\theta \sum_{i=1}^{n} (y_i - \theta^T x_i)^2 + \lambda ||\theta||^2 \end{align}

参考

【机器学习我到底在学什么】哲学角度聊聊贝叶斯派和频率派，数学角度看看极大似然估计和最大后验估计 https://www.bilibili.com/video/BV1Ea4y1J7Jq

机器学习-白板推导系列(一)-开篇 https://www.bilibili.com/video/av31950221

李航《统计学习方法》

周志华机器学习

PRML

MLAPP

《ESL》

《Deep Learning》

台大林轩田《机器学习基石》/《机器学习技法》（SVM） / 《VC理论》

张志华《统计机器学习》（贝叶斯）/《机器学习导论》（频率派）

Stanford Andrew Ng CS229 CS330

徐益达概率模型，github notes

台大李宏毅 ML 2017 / MLDS 2018

正态分布 $N(\mu, \sigma^2)$ 概率密度函数

$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp{(-\frac{(x-\mu)^2}{2\sigma^2})}$

拉普拉斯分布 $L(\mu,b)$ 概率密度函数

$f(x|\mu,b)=\frac{1}{2b}\exp(-\frac{|x-\mu|}{b})$

Attention

Posted on 2020-01-28

注意力机制的演化

RNN

N vs N

输入输出等长

$$ h_i = f(ax_i + bh_{i-1} + c) $$

N vs 1

输入 N 输出 1

1 vs N

输入 1 输出 N

N vs M / Encoder-decoder / Seq2seq(变长)

输入 N 输出 M，如翻译问题，输入输出的单词不等长。

Encoder 将输入编码为 c，再作为输入传入 decoder。

LSTM

LSTM 为了解决 RNN 梯度消失问题，在 RNN 结构的基础上：

增加了遗忘门，一定概率遗忘上一层隐藏层的状态：

GRU

RNN + Attention (Encoder-decoder)

Attention机制通过在每个时间输入不同的c来解决问题

下图是带有 attention 机制的 decoder

以 encoder-decoder 翻译任务为例，输入的序列是“我爱中国”，因此，Encoder中的 $h_1$ 、 $h_2$ 、 $h_3$ 、 $h_4$ 就可以分别看做是“我”、“爱”、“中”、“国”所代表的信息。在翻译成英语时，第一个上下文 $c_1$ 应该和“我”这个字最相关，因此对应的 $a_{11}$ 就比较大。 $c_2$ 应该和“爱”最相关，因此对应的 $a_{22}$ 就比较大。最后的 $c_3$ 和 $h_3$ 、 $h_4$ 最相关，因此 $a_{33}$ 、 $a_{34}$ 的值就比较大。

Attention QKV

以下是 attention 机制单独使用的例子。

输入 $q$ ，Memory 中以 $(k,v)$ 形式存储需要的上下文，其中 $k$ 是 question， $v$ 是 answer， $q$ 是新来的 question，根据与 $q$ 相似的历史 $k$ ，带权 $v$ 求和，输出 $c$ 。

计算步骤

在 Memory 中寻找相似 k（score function）： $e_i = a(q,k_i)$ $e i = a (q, k i )$ ，其中 $a$ $a$ 是打分函数（注意力分布），可选：
1. 加性模型 $a(q,k_i)=v^T\tanh (Wk_i + Uq)$
2. 点积模型 $a(q,k_i)=k_i^Tq$
3. 缩放点积模型 $a(q,k_i)=\frac{k_i^Tq}{\sqrt{d}}$
4. 双线性模型 $a(q,k_i)=x_i^TWq$
归一化（alignment function）： $\alpha = softmax(e)$
读取内容（context vector function）： $c = \sum_i \alpha_i v_i$

数化简成一个公式：（打分函为缩放点积模型）

$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt d_k})V$

其中 $Attention(Q,K,V)\in \mathbb R^{n\times d_v},Q\in\mathbb R^{n\times d_k},K\in\mathbb R^{m \times d_k}, V\in\mathbb R^{m\times d_v}$

Self-attention

Q K V 均来自统一输入

Traditional Attention

$Attention(Q)=softmax(W^T U^T Q)\cdot Q$

Attention 总结

计算区域

Soft attention：对所有key求权重，进行加权

Hard attention：对一个 key 权重为 1，其余权重为 0。无法求导，因此需要用强化学习。

Local attention：用 hard 方法定位到一个区域，区域内用 soft 方法

所用信息

Genreal attention：

Local attention：

Self attention：如 AutoInt

结构层次

单层 attention：常用方法，用一个 query 对一段原文进行一次 attention

多层 attention：一般用于文本具有层次关系的模型，假设我们把一个document划分成多个句子，在第一层，我们分别对每个句子使用attention计算出一个句向量（也就是单层attention）；在第二层，我们对所有句向量再做attention计算出一个文档向量（也是一个单层attention），最后再用这个文档向量去做任务。

多头 attention：《Attention is All You Need》用到了多个query对一段原文进行了多次attention，每个query都关注到原文的不同部分，相当于重复做多次单层attention

模型

CNN + attention：

LSTM + attention：

相似度计算

点乘： $s(q,k)=q^T k$

矩阵相乘： $s(q,k)=q^T k$

cos 相似度： $s(q,k)=\frac{q^T k}{|q|\cdot|k|}$

串联方式： $s(q,k)=concat(q,k)$

MLP： $s(q,k)=v^T \tanh(aq + bk)$

参考

https://zhuanlan.zhihu.com/p/91839581

https://zhuanlan.zhihu.com/p/85038315

蘑菇街推荐算法之迷——Self Attention不如Traditional Attention？ https://mp.weixin.qq.com/s/3nTevkiLLaZ6eX7nZWzvTg

dnn-tricks

Posted on 2020-01-08

DNN 如何调优？

欠拟合

增加模型深度：ResNet20 -> ResNet50
微调结构：更小的 feature map & pooling size
更换复杂网络：AlexNet -> ResNet -> …
DeepCTR 模型使用高阶特征交叉（DCN、xDeepFM）
梯度弥散：BatchNorm

过拟合

数据预处理：不平衡类别；异常值剔除；PCA / ZCA Whitening 或者 BatchNorm；加入噪音增强模型鲁棒性
数据扩增：加入噪音；图片旋转、平移、剪裁、颜色、调色；SMOTE；合成样本；使用外部数据
迁移学习：在 ImageNet VGG 基础上训练，根据数据分布决定是否冻结权重
正则化：L1、L2
Dropout
早停
多目标学习：ESMM
半监督学习：无标注样本假设（平滑假设、聚类假设、流形假设）
迁移学习
多模态学习
对抗训练：GAN，合成对抗样本

精度提升

初始化：全0、随机、he_normal() $mean=0,var=sqrt(2/fan\_in)$ 、glorot_normal() $mean=0,var=sqrt(2 / (fan\_in + fan\_out))$
学习率：微调，Adagrad Adam 自适应学习率的优化方法
激活函数
损失函数
组合模型：Bagging 或 Boosting；CV；同一模型多次初始化训练
样本不平衡：负样本降采样；设置类权重；2-stage 分类任务；单独在少数类别样本上微调
特征工程：Embedding

附录

范数

损失函数中，正则项一般是参数的 Lp 距离。向量 x 的范数，指原点到 x 的距离。

L1最优化问题的解是稀疏性的, 其倾向于选择很少的一些非常大的值和很多的insignificant的小值. 而L2最优化则更多的非常少的特别大的值, 却又很多相对小的值, 但其仍然对最优化解有显著的贡献. 但从最优化问题解的平滑性来看, L1范数的最优解相对于L2范数要少, 但其往往是最优解, 而L2的解很多, 但更多的倾向于某种局部最优解.

L0范数本身是特征选择的最直接最理想的方案, 但如前所述, 其不可分, 且很难优化, 因此实际应用中我们使用L1来得到L0的最优凸近似. L2相对于L1具有更为平滑的特性, 在模型预测中, 往往比L1具有更好的预测特性. 当遇到两个对预测有帮助的特征时, L1倾向于选择一个更大的特征. 而L2更倾向把两者结合起来.

lp-balls

L0-范数

$d=\sum_{i=1}^{n}\bigg(x_i^{0}\bigg)^{\frac {1}{0}}$

向量中非零元素的个数

在 Sparse Coding 中, 通过最小化 L0 寻找最少最优的稀疏特征. 但难以优化, 一般转化成 L1 L2

L1-范数

曼哈顿距离

$d=\sum_{i=1}^{n}\bigg|x_i-y_i\bigg|$

如计算机视觉中对比两张图片的不同像素点之和

L2-范数

欧几里得距离

$d=\sum_{i=1}^{n}\bigg(|x_i-y_i|^{2}\bigg)^{\frac {1}{2}}$

Lp-范数

$d=\sum_{i=1}^{n}\bigg(|x_i-y_i|^{p}\bigg)^{\frac {1}{p}}$

无限范数距离

切比雪夫距离

d = \lim_{p \to \infty}\sum_{i=1}^{n}\bigg(|x_i-y_i|^{p}\bigg)^{\frac {1}{p}} = \max(|x_1-y_1|,…,|x_n-y_n|)

损失函数

0 - 1 损失函数

gold standard

$L_{01}(m)=\begin{cases} 0 &\text{if } m \ge 0 \\ 1 &\text{else} \end{cases}$

对数损失函数

Log Loss, cross entropy error

$L(Y,P(Y|X))=-\log P(Y|X)$

对 LR 而言, 把它的条件概率分布方程

$P(Y=0|X)=\frac {1}{1+e^{wx+b}}, P(Y=1|X)=1-P(Y=0|X)$

带入上式, 即可得到 LR 的对数损失函数

平方损失函数

Square Loss

$L(Y,P(Y|X))=\sum_{i=1}^{n}(Y-f(X))^2$

其中 $Y-f(X)$ 表示残差, 整个式子表示残差平方和, Residual Sum of Squares

指数损失函数

Exponential Loss

$L(Y,f(X))=e ^ {-Y f(X)}$

如 Adaboost, 它是前向分步加法算法的特例, 是一个加和模型, 损失函数就是指数函数. 经过m此迭代之后, 可以得到

$f_m(x)=f_{m-1}(x)+\alpha_mG_m(x)$

Adaboost 每次迭代的目标是最小化指数损失函数

${\arg\ \min}_{\alpha, G}=\sum_{i=1}^{N}e^{[-y_i(f_{m-1}(x_i)+\alpha G(x_i))]}$

合页损失

Hinge Loss, 如 SVM

$L(Y,f(X))=max(0,1-Y * f(X)), Y=\{0,1\}$

含义是样本被正确分类且函数间隔大于1时,损失时0; 否则损失是 $1-Y f(X)$ . 当分类正确且确信度足够高时, 损失才是0, 对学习有更高的要求.

Huber 损失

常用于回归树。与比平方损失相比，它对 outlier 更加不敏感

对于回归问题

$L_{\delta}(a) = \begin{cases} \frac{1}{2} a^2 &\text{for } |a| \le \delta,\\ \delta \big( |a| - \frac{1}{2} \delta \big) &\text{otherwise.} \end{cases}$

其中 $|a|=y-f(x)$

对分类问题

$L_{\delta}\big(y, f(x)\big) = \begin{cases} \frac{1}{2} \big(y-f(x)\big)^2 &\text{for } \big|y-f(x)\big| \le \delta,\\ \delta \big|y-f(x) \big| - \frac{1}{2} \delta^2 &\text{otherwise.} \end{cases}$

下图是 huber loss（绿色）与平方损失（蓝色）的对比，来自 wiki

正则化

Regulization or Penalization：

${\min}_{w \in \Theta}\frac{1}{N}\sum_{i=l}^{N}L(y_i,f(x_i,w))+\lambda J(w)$

其中第一项是经验风险, 第二项是正则化项。常见的正则项，通过 $L_0,L_1,L_2$ 范数衡量参数 $w$ ，有

$J_0(w) = \big|\{i:w_i \ne 0\}\big|$

$J_1(w) = \sum_i |w_i|$

$J_2(w) = \frac{1}{2} ||w||^2$

其中 $L_2$ 正则项最常用，因为它是凸函数，可以用梯度下降法求解。

而 $L_1$ 正则项有特征选择功能，能够得到更加稀疏、更多 0 的解。可以用简单截断法，梯度截断法（TG, Truncated Gradient），ADMM 方法求解。

以 $w\in \mathbb R^2$ 为例，椭圆形是 loss 的损失等高线，灰色区域是约束区域，等高线与约束区域相交的地方，就是最优解。可以看出，L1 较 L2 有更大的概率在角处相交，得到稀疏解。

l1vsl2

Batch Norm

Internal Covariate Shift 定义：在深层网络训练的过程中，由于网络中参数变化而引起内部结点数据分布发生变化的这一过程被称作Internal Covariate Shift。

常见的方法有对每层输入做 Whitening，保留彼此不相关的特征（耗时），然后使其具有相同的均值和方差（同分布）：

# compute the SVD factorization of the data covariance matrix
U,S,V = np.linalg.svd(cov)
# decorrelate the data
Xrot = np.dot(X, U) 
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)

BN 改进了 Whitening 计算耗时的问题，退而求其次，对每个特征进行标准化，使其具有均值为0，方差为1的分布。

编辑距离

指两个字串之间，由一个转成另一个所需的编辑操作次数，包括：

Levenshtein距离：可以删除、加入、取代字符串中的任何一个字元

LCS（最长公共子序列）距离：只允许删除、加入字元

Jaro 距离：只允许字符转置

汉明距离：只允许取代字元

Jaccard 距离

$J(A,B) = \frac{A \cap B}{A \cup B}$

余弦相似性

$dist(A, B)=\cos\theta =\frac{A \cdot B}{||A||\times||B||}$

余弦距离衡量两个向量的夹角。当向量是用户评分时，可以自动做评分尺度归一。比如 $dist((1,1) (3,3)) == dist((1,1),(5,5))$

0度角的余弦值是1，而其他任何角度的余弦值都不大于1；并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。这结果是与向量的长度无关的，仅仅与向量的指向方向相关。余弦相似度通常用于正空间，因此给出的值为0到1之间。

淘宝 oCPC 算法笔记

Posted on 2019-10-14

背景

常见广告计费方式：

CPM / CPC：固定出价，标签定向，缺点是无法最优化广告主利益
oCPM：Facebook，微信朋友圈，优化广告主利益，广告主承担点击转化风险
oCPC：淘宝，同时优化三方利益（广告平台收入、广告主利益、用户体验），广告平台承担点击转化风险
oCPA：腾讯广告，同时优化三方利益，需要学习，更多时间起量，广告平台承担注册转化风险

淘宝广告与一般 RTB 相比：有用户全生命周期的数据；大部分中小广告主，关注收入而不是品牌曝光，因此提升 GMV 可以惠及广告主；统一 CPC 结算；以 GMV 为优化指标，同时满足三者的利益，达到多赢局面。

淘宝使用 oCPC 原因：CPS CPA 忽视点击价值，结算效率低；CPM 对中小广告主有更高风险，因为 CPC 使广告主可以控制点击成本，而淘宝承担曝光 - 点击转化风险。综合考虑生态和效率，淘宝使用 CPC 结算。

建模

优化目标：GMV 或 GMV + 广告收益

优化约束：出价区间与 ROI 相关

广告主 ROI 公式（出价约束）

$\begin{aligned} roi_{u,a} &= \frac{p(c|u,a) v_a}{b_a} \\ roi_a &= \frac{v_a \sum_u n_u p(c|u,a)}{b_a \sum_u n_u} = \frac{E_u[p(c|u,a)] v_a}{b_a} \end{aligned}$

其中：

$p(c|u,a)$ 是给定广告 a 用户 u 的点击率预估

$v_a$ 是预测用户购买付费，PPB (predicted pay-per-buy)

$b_a$ 是广告主出价

$n_u$ 是用户一段时间的总点击次数

$E_u[\cdot]$ 认为是常量

出价区间百分比 $\frac{b^*_a}{b_a}$ 关于 $roi_a$ 的函数如下

其中 $r_a$ 是阈值避免出价区间过高带来损失，本文 40%。

可从上图推出最优出价 $b^*_a$ 的上界是 $l(b^*_a)$ 下界是 $u(b^*_a)$

优化目标

$\begin{aligned} \max_{b^*_1,b^*_2,...,b^*_n} &f(b^*_k) \\ s.t.\ \ \ &k = \arg \max_i pctr_i \times b^*_i \\ & l(b_i^*) \le b_i^* \le u(b_i^*), i = 1,...,n \\ \end{aligned}$

其中 $f$ 有两种定义： $f_1$ 是 GMV 最大化， $f_2$ 加入广告收入作为目标一部分。

$\begin{aligned} f_1(b_k^*) &= pctr_k \times pcvr_k \times v_k \\ f_2(b_k^*) &= pctr_k \times pcvr_k \times v_k + \alpha \times pctr_k \times b_k^* \end{aligned}$

排序算法

给定候选广告，每个广告出价满足出价约束，有排序算法如下。

其中每个迭代选出 top i 广告，同时确保剩余广告以最低价出价。

Input: Ad list A, corresponding boundaries of bid price
Output: Optimized bid prices b∗a for ∀a∈A
A=∅;
repeat
       Sort ads in A in descending order of f(i,u(b∗i));
       t← the largest l(s∗a) for ∀a∈A;
       Find the first ad k from A that u(s∗k)≥t;
       A=A∪{k};
       A=A∖{k};
       for i∈A do
             u(s∗i)=min(u(s∗i),u(s∗k));
             u(b∗i)=min(u(b∗i),u(s∗i)pctri);
       end for
until ∥A∥==N or A==∅;
for i∈A∪A do
       b∗i=u(s∗i)pctri;
end for
Return b∗a for each ad in A∪A;

参考

KDD17’ Optimized cost per click in taobao display advertising

graph-embedding

Posted on 2019-07-09

Network Embedding

Item2vec

Barkan et. al. 在 ICML16 Workshop 提出，区别于 item2item （ALS ItemCF）方法，用 word2vec （负采样 Skip-gram）学习物品隐式表达。

以用户浏览商品作为句子。假设同句子中的词是无顺序关系的，忽略了浏览顺序的 spartial information。其他情况可能不符合该假设，比如丛书《哈利波特1-5》。

Music 领域分类，用音乐人流派进行聚类， item2vec 方法与 SVD 对比，有效分类：

Airbnb Embedding

KDD 18 Real-time Personalization using Embeddings for Search Ranking at Airbnb (Airbnb 2018)

对用户和房源计算 word2vec，embedding everything，提升搜索推荐系统的性能。

Graph Embedding

目标是用低维稠密向量表示图中的点。解决传统方法问题：

矩阵分解 — 计算量大
构造人工特征 — 需要领域知识、工作量大

可用于推荐、节点分类、链接预测、可视化等场景。

DeepWalk

刻画节点在图上的近邻性 —— 在 1- W步的随机游走过程中，两个节点能到达的概率。

构造无向无环图，以特定点作为起点，做随机游走得到点的序列作为句子，用 w2v skip-gram 学习。

例如给定 KV 对（用户，APPID），计算 APPID 的 embedding 时，以 APPID 作为节点，两个 APPID 之间共同的用户占比作为权重。

LINE

《LINE: Large-scale Information Network Embedding WWW15》MSRA PDF

是 DeepWalk 仅游走 1 、2 步的带权重版本，为性能考虑做了一些优化。

利用图中已存在的边构造目标函数，该目标函数显式描绘了一阶（6 和 7）和二阶（5 和 6）的邻近关系。然后通过优化方法去学习点的表达向量，其本质上是一种关于边的平滑，即很多很可能存在的边实际上不存在，需要模型去学习和预测出来。

一阶优化目标

对每一条无向边 $(i,j)$ ，定义顶点 $v_i,v_j$ 的联合概率为

$p_1(v_i,v_j)=\sigma(-u_i^T \cdot u_j)$

其中 $u_i$ 为 $v_i$ 的低维向量表示， $w_{ij}$ 是边权。

同时定义经验分布

$\hat {p_1} = \frac{w_{ij}}{\sum_{i,j\in E} w_{ij}}$

优化目标为

$\min O_1 = d(\hat{p_1(\cdot,\cdot)}, p_1(\cdot,\cdot))$

其中 $d(\cdot,\cdot)$ 是两个分布的距离，常用 KL 散度。设 p 为真实分布，q 为近似分布， KL散度是用来度量使用基于 q 的分布来编码服从 p 的分布的样本所需的额外的平均比特数：

$KL(p||q)=\sum p(x_i) (\log p_i - \log q_i)$

如果使用 KL 散度并忽略常数项，则有

$\min O_1= -\sum_{i,j \in E} w_{ij} \log p_1(v_i,v_j)$

二阶优化目标

这里对于每个顶点维护两个embedding向量，一个是该顶点本身的表示向量，一个是该点作为其他顶点的上下文顶点时的表示向量。

对于有向边 $(i,j)$ ，定义给定顶点 $v_i$ 条件下，产生上下文(邻居)顶点 $v_j$ 的概率为

$p_2(v_j|v_i) =\frac{\exp(u_j^T \cdot u_i)}{\sum_{k=1}^{|V|} \exp(u_k^T \cdot u_i)}$

定义经验分布

$\hat{p_2}(v_j|v_i) = \frac{w_{ij}}{d_i}$

其中 $w_{ij}$ 是边权， $d_i$ 是定点 $v_i$ 的出度。对于带权图，有

$d_i=\sum_{k\in N(I)}W_{ik}$

优化目标为

$O_2 = \sum_{i\in V}\lambda_i d(\hat{p_2}(\cdot|v_i), p_2(\cdot|v_i))$

其中 $\lambda_i$ 为控制节点重要性的因子，可以通过顶点的度数或者 PageRank 等方法估计得到。

带入 KL 散度并设 $\lambda_i = d_i$ ，忽略常数项，有

$O_2=-\sum_{i,j\in E} w_{ij} \log p_2(v_j|v_i)$

对于用户ID-游戏ID 序列能够较好的建模。

https://zhuanlan.zhihu.com/p/56478167

Node2Vec

Standford16，在 DeepWalk 的基础上更进一步，通过调整随机游走权重的方法使 graph embedding 的结果在网络的 同质性（homophily）和结构性（structural equivalence）中进行权衡。

为了使 Graph Embedding 的结果能够表达网络的同质性，在随机游走的过程中 BFS 产生结构性，DFS 产生同质性。为了获取二者的特性，通过 1/p 和 1/q 参数控制随机游走过程往远处跳、跳回的概率。

从实验结果看，同质性相同的物品很可能是同品类、同属性、或者经常被一同购买的物品，而结构性相同的物品则是各品类的爆款、各品类的最佳凑单商品等拥有类似趋势或者结构性属性的物品。

Metapath2vec

改进 LINE，通过 metapath，解决以构图在多种类型节点之间保存上下文概念，目标函数

$\arg \max_\theta = \sum_{v\in V} \sum_{t\in T_V} \sum_{c_t \in N_t(v)} \log p(c_t|v;\theta)$

其中 $N_t(v)$ 表示顶点 $v$ 的邻居（第 $t$ 类型）， $p$ 是 softmax 函数。

在 Metapath2vec 中，softmax 函数是在所有节点无论什么类型上进行归一化：

$p(c_t|v;\theta)=\frac{e^{X_{e_t}} e^{X_v}}{\sum_{u\in V} e^{X_u}e^{X_v}}$

在 Metapath2vec++ 中，softmax 函数是在相同类型节点上进行归一化：

$p(c_t|v;\theta)=\frac{e^{X_{e_t}} e^{X_v}}{\sum_{u_t \in V} e^{X_{u_t}}e^{X_v}}$

为加速运算，用 Heterogeneous negative sampling 优化，目标函数：

$O(X)=\log\sigma(X_{c_t}\cdot X_v) + \sum_{k=1}^{K}\mathbb E_{u_k^t\sim P_t(u_t)}[\log \sigma(-X_{u_t^k} \cdot X_v)]$

https://zhuanlan.zhihu.com/p/32598703

BiNE

《BiNE: Bipartite Network Embedding SIGIR18》 PDF

当尝试把 DeepWalk 方法应用于二部图上时，会出现两个问题:

DeepWalk算法适用于同质网络，而二部图则是一个天生的异质网络，二部图的边连接了左右两种不同类型的节点。同时，目前的网络嵌入方法基本没有考虑去建模图中的隐式关系。
DeepWalk的随机游走策略限制了对数据的采样，一是以每个节点为起点的游走序列的数量都相同，二是得到的这些序列的长度也都是相同的，这样会导致采集来的数据的分布与真实的数据分布会存在差异，如下图所示

虽然目前也有应用于异质网络上的模型如 metapath2vec，且我们可以认为二部图是一种特殊的异质网络，但这些模型也都有缺陷，比如metapath2vec++，它视显式关系与隐式关系在节点表示学习中同等重要，这点与我们的常识相悖，一般来讲，显式关系的重要性是要大于隐式关系的。

论文提出的BiNE模型首先进行有目的性的随机游走(random walk)，生成节点序列。然后设计一种既考虑了显式关系(explicit relations),又考虑到了隐式关系(implicit relations)的新型优化框架，来学习节点的表示。

显式关系，就是指能从数据集中直接获得的关系信息，如图中可观测到的边的信息。

隐式关系，就是指数据中隐含的关系信息，例如两个节点间虽然并没有边相连，但它们连接了同一个节点，我们就有理由认为这两个节点之间存在着某种隐式关系。

实验结果：BiNE 优于 LINE 和 metapath2vec++

https://zhuanlan.zhihu.com/p/83412062

M2GRL

《M2GRL: A Multi-task Multi-view Graph Representation Learning Framework for Web-scale Recommender Systems KDD2020》PDF

深度传送门

EGES

KDD18 Enhanced Graph Embedding with Side Information，为了使“冷启动”的商品获得“合理”的初始Embedding，阿里团队通过引入了更多补充信息 (side info) 来丰富Embedding信息的来源，从而使没有历史行为记录的商品获得Embedding，模型演进 DeepWalk -> BGE -> GES -> EGES。

Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba

BGE

通过 user 短期行为序列构建有向有权图，节点是 item，通过 Skip-Gram 学习 embedding。

GES

在 BGE 基础上，加入 item 的额外信息（category brand price 等）作为 words，通过 Skip-Gram 训练得到 embedding。

对每个 item，有 item_emb / cat_emb / bran_emb / price_emb，用这些 embedding 均值作为 item 的表达。

$H_v=\frac{1}{n+1}\sum_{s=0}^{n}W_v^s$

EGES

在 GES 基础上，引入了 attention 机制，对每个 dense embedding 增加可训练的权重，并做 softmax 归一化

$H_v=\frac{\sum_{j=0}^{n}\exp(a_v^j) W_v^j}{\sum_{j=0}^{n} \exp(a_v^j)}$

应用 Weighted Skip-Gram 方法学习模型参数。

https://blog.csdn.net/google19890102/article/details/108863046

SDNE

THU16 本文认为，DeepWalk 的缺点是缺乏明确的优化目标，即objective function，而LINE是把网络的局部信息和全局信息分开学习，最后简单地把两个表达向量连接起来，显然不是最优做法，文章利用深度学习去做graph embedding，好处自然是非线性表达能力更强了，然后设计了一个同时描述局部和全局网络信息的目标函数，利用半监督的方式去拟合优化。

SimRank

MIT 02 Jeh & Widom 提出，给定 user-item 二部图 $G(V,E)$ ，考虑如果用户相似，那么他们关联的物品也相似。其中 V 是节点，E 是边。

定义两个节点的相似度

$s(a,b)=\frac{C}{|I(a)||I(b)|}\sum_{i=1}^{|I(a)|} \sum_{j=1}^{|I(b)|} s(I_i(a), I_i(b))$

如果 a = b 则 $s(a,b)=1$ ；如果 $a\ne b,I(a)\ne null,I(b)\ne null$ 则结果如上式；其他情况 $s(a,b)=0$

其中 $I(a)$ 表示和 a 相连的二部图另一个子节点的集合。

SimRank++

SimRank++算法对SimRank算法主要做了两点改进。第一点是考虑了边的权值，第二点是考虑了子集节点相似度的证据。

User2vec LSTM

Graph Conv Network

https://zhuanlan.zhihu.com/p/74345718

GraphSAGE

《Inductive Representation Learning on Large Graphs NIPS17》PDF

https://zhuanlan.zhihu.com/p/62750137

https://zhuanlan.zhihu.com/p/74242097

图网络内节点表达的学习，已在多项任务中被证明了其实用性，如传统的Deepwalk、Semi-GCN等方法。但是，目前大多数已存在的方法，在训练过程中都仅仅考虑当前的节点，学习目标也是直接生成当前节点的embedding，而对未知的节点，并不能起到泛化的作用。也就是说，目前的大部分方法，都是transductive式学习。

为了解决对未知节点的泛化问题，本文提出了GraphSAGE的方法，它采用的是inductive的学习模式，在GCN基础上，通过训练聚合邻居节点的函数，使得GCN扩展成inductive学习的任务，对未知节点起到泛化作用。

http://km.xx.com/group/24938/articles/show/404557

斯坦福大学的JureLeskovec团队在NIPS017提出了GraphSage 模型，通过以下两方面的改进来解决掉上述原始GCN的两个缺陷：（1）不是直接对全图进行卷积，而是通过对目标节点的邻居进行随机采样得到子图，再对子图进行卷积，大大降低了计算和内存的压力。（2）不是直接学习网络节点的embedding，而是学习一个聚合函数（aggregator）,这个聚合函数能够把邻居节点的特征聚合到中心节点的身上。当我们学习出聚合函数后，就可以泛化到新的节点或者新的网络上，即使是在训练过程中模型没有见过的节点也能推断出其embedding，是一种归纳式（inductive）学习算法。GraphSage的算法架构如下图所示分为三个步骤：

对图中的每个节点采样固定数量的邻居节点作为该节点的邻居节点集合。
通过模型学习的聚合函数（aggregator）对步骤1中采样得到的邻居节点集合进行聚合，把邻居集合节点的特征信息聚合到中心节点上，得到新的节点Embedding。
由步骤2邻居聚合得到的新的节点embedding用来进行下游的预测任务。

GAT

《GRAPH ATTENTION NETWORKS ICLR18》 PDF

GraphSAGE 在聚合邻居节点过程中，将其都视作相同的贡献度有些粗糙与不合理，因此本文引入注意力机制到图神经网络中，每一层学习节点的每个邻居对其生成新的特征的贡献度，按照贡献度大小对邻居特征进行聚合，以此来生成新的聚合特征，供下游任务使用。

H-GCN

《Hierarchical Graph Convolutional Networks for Semi-supervised Node Classification 19》PDF

GCN的相关方法尽管在网络挖掘任务中取得了巨大成功，但大多数基于邻居聚合特征的方法，通常层数都比较浅，且缺乏graph pooling的机制，使得其很难获得充足的网络的全局信息。因此，为了扩大卷积层的感受野，本文提出了深度层次的GCN网络来机型semi-supervised的节点分类任务。（由于超点对应了原始图的局部结构，对超节点组成的超图进行卷积，也就获得了更大的感受野）

GraphRT

《Graph Neural Network for Tag Ranking in Tag-enhanced Video Recommendation CIKM20》PDF

https://zhuanlan.zhihu.com/p/279287735

微信的GraphTR模型的思路：

GraphTR是为了要学习优质tag embedding，为此要注重利用用户的行为信息。但是由于user-tag的行为太稀疏，因此GraphTR需要通过user-video的行为学习到tag embedding。要达成以上目标，也有多种作法。

GraphTR的做法是：

将user, video, tag（还加上video的来源media）都放入一个大的异构图

通过图卷积，学习到video embedding，再建模video与video之间的相关性（比如在同一个session中播放过

因为video embedding融合了tag embedding，因此在优化目标达成之后，一个优质的副产品就是得到tag embedding。

构建图

图上要包括：user, video, tag, media (视频来源)这 4类节点。因为用户数目太多，而每个用户的行为相对稀疏，GraphTR将用户按照gender-age-location分成84000组，用user group替代user，在图中建模。

而图上要包括以下5类边（这一版本暂时不考虑边上的权重）：

video-video：同属一个观看session中的两video之间有边

user-video：某视频被某user group一周观看超过3次。 (因为user-tag行为稀疏，因此图中没有user-tag的边)

video-tag：video和其携带的tag

video-media：video和其来源

tag-tag：两个 tag属于同一个视频
聚合异构节点

为了完成user, video, tag, media这四类节点的信息融合，GraphTR 设计了3层卷积结构，称为Heterogeneous field interaction network (HFIN)。
建模节点相关性

建模video-video之间的相关性，在同一个session被观看的视频之间，距离要尽可能小。因为video的点击行为比较多，这方面的数据比较丰富，文中采用的是这种方案。loss 使用 w2v
应用 tag emb

拿用户观看过视频携带的tag的embedding加权平均得到user embedding，再拿这个user embedding在当前视频所携带的tag的embedding中寻找出距离最近的top-k个tag，作为推荐结果显示在视频的下方。因为这些tag embedding蕴含了丰富的user-video行为信息，不仅有助于提升用户对tag的点击率，也有助于提升进入沉浸式tag频道后的观看时长。

总结：

微信团队面临的是，数据少的领域如何借力于数据多的领域，同时要兼顾两个领域的优化目标。而他们没有采取传统的“迁移+多目标”的方式，而是通过将不同领域的不同节点、关系建立在一张异构图上，通过图卷积，使得每个节点的embedding都浓缩了多个领域的知识，达成了“知识迁移+目标兼顾”。GraphTR在微信这种大规模推荐场景下的成功运用，展现了GNN在迁移学习、多任务学习方面的强大能力，为我们解决类似问题提供了全新的思路。

GraphTR 采用了GraphSAGE+FM+Transformer多种手段，粒度上从粗到细，交叉、聚合来自不同领域的异构消息，相比于mean/max pooling、浅层FC等传统聚合方式，极大提升了模型的表达能力，值得借鉴。

下图结构：

首先定义目标节点，找出一跳二跳的节点。

1 agg layer 输入二跳节点，输出一跳节点的 emb

2 agg layer 输入一跳节点 emb，经 avg pool 输出 target node 的 emb

所有异构节点共享 emb 空间，表征用户偏好，相邻节点空间相近。

loss 衡量临近相似度，好处是最大化利用视频相关行为和profile，学习用户在 video 的偏好，同时学到用户在 tag 偏好。

正例：被相同用户看过的两个视频 / 相同tag的两个视频 / 相同media的两个视频

$J = -\sum_{o_i}\sum_{o_k\in N_i}\sum_{o_k\notin N_i} \log (\sigma(o_i^T o_k)) + \log(\sigma (o_i^T o_j))$

计算框架

Tencent Angel

https://github.com/Angel-ML/angel 腾讯 PS 计算框架，支持推荐算法和图网络算法：

1
2
3

图挖掘: PageRank、Kcore、Closeness，共同好友、三角结构、社团发现、其他；
图神经网络: GCN、GraphSage、DGI等神经网络算法；
图表示学习: LINE、Node2Vec算法。

TI-ML

https://tesla.xx.com/gitbook/doc/graph/tdw-ml-tx_graph-vital_nodes_identification.html 腾讯云算法平台，支持图算法

社团发现
	FastUnfolding
	LPA
	HANP
	COPRA
节点重要性评价
	PageRank
	KCore
链路预测
	AdamicAdar
	ResourceAllocation
图特征指标
	HyperAnf
	GlobalClusterCoefficient
图表示学习
	LINE
	Node2vec
	Word2vec
其他
	CommonFriends
	ConnectedComponent
	ReIndex
	Sample
	EffectiveSize

Wechat Plato

https://github.com/Tencent/plato 微信图计算框架，支持算法有：

图特征
	树深度/宽度
	N-阶度
	HyperANF
节点中心性指标
	KCore
	Pagerank
	Closeness
	Betweenness
连通图 & 社团识别
	Connected-Component
	LPA
	HANP
图表示学习
	Node2Vec-Randomwalk
	Metapath-Randomwalk
	聚类/分圈算法
ConnectedComponents
	FastUnfolding
	其他图相关算法
	BFS
	共同类计算
Incoming
	Word2Vec, Line, GraphViteGCN 相关

https://git.code.xx.com/TencentGraph/PlatoEmbedding

https://tesla.xx.com/react/index.html#/algorithm-market/home

Alibaba Euler

https://github.com/alibaba/euler/ 阿里图计算框架，支持算法：

LsHNE

https://github.com/alibaba/euler/wiki/LsHNE

针对搜索广告召回的大规模异构网络Embedding方法。

解决 NE 在淘宝数据集上的挑战：节点、边类型丰富；向量距离敏感；节点属性未利用的

无监督，样本采样 Node2vec Walk ，目标

LasGNN

https://github.com/alibaba/euler/wiki/LasGNN

ScalableGCN

https://github.com/alibaba/euler/wiki/ScalableGCN

Reference

[0] https://zhuanlan.zhihu.com/p/33732033

[1] DeepWalk: Online Learning of Social Representations

[2] LINE: Large-scale Information Network Embedding

[3] node2vec: Scalable Feature Learning for Networks

[4] Structural Deep Network Embedding

[5] 深度学习中不得不学的Graph Embedding方法 https://zhuanlan.zhihu.com/p/64200072

[7] Item2Vec: Neural Item Embedding for Collaborative Filtering https://arxiv.org/abs/1603.04259

假设检验

Posted on 2019-06-12

假设检验

基本步骤

提出原假设 $H_0$ 和备择假设 $H_1$
考虑检验中对样本做出的统计假设；例如，关于独立性的假设或关于观测数据的分布的形式的假设
确定适当的检验统计量 $T$ wiki
在零假设下推导检验统计量的分布。在标准情况下应该会得出一个熟知的结果。比如检验统计量可能会符合 t-分布或正态分布
选择一个显著性水平 $\alpha$ ，若低于这个概率阈值，就会拒绝零假设。常用 5% 和 1%
根据在零假设成立时的检验统计量 $T$ 分布，找到数值最接近备择假设，且几率为显著性水平 $\alpha$ 的区域，此区域称为“拒绝域”，意思是在零假设成立的前提下，落在拒绝域的几率只有 $\alpha$
针对检验统计量 $T$ ，根据样本计算 / 查表得到其估计值 $t_{obs}$ 和 $p-value$
若估计值 $t_{obs}$ 落在“拒绝域”（如 $p < \alpha$ ），接受对立假设；反之接受零假设

检验统计量

检验统计量, test Statistic wiki，是一个从样本推导出来的统计量，用于假设检验。

Chi-Square Test

适用问题：统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越小；反之，二者偏差越大，若两个值完全相等时，卡方值就为0，表明理论值完全符合。其中卡方检验针对分类变量。

例：两组数据转化率是否一致？男性、女性对线上买生鲜食品的行为有没有区别？

ANOVA F-test

ANalysis Of VAriance，方差分析，又称变异数分析，F-test。

适用问题：判断两组来自正态分布总体的样本，方差是否相同。

一般在双样本 T-test 前使用：若两总体方差相等，则直接用 t-test；若不等，可采用 Welch’s t-test 或变量变换或秩和检验等方法。

import scipy.stats
print(scipy.stats.f_oneway([1,2,3], [3,2,1], b))
# F_onewayResult(statistic=0.0, pvalue=1.0)
# F-statistic = variance between groups / variance within groups

如果样本非来自正态分布总体，可以使用 Levene’s test or Bartlett’s test 算法。

Z-test

适用问题：两组大样本（大于30）正态分布数据，均值之差是否为某一实数。

原理：用标准正态分布的理论来判断差异发生的概率，从而比较两个平均数>平均数的差异是否显著。

例：王者荣耀男性、女性用户，人均付费是否有显著差异？

T-test

适用问题：【一组 | 两组】来自正态分布总体的独立样本，其中样本数小于 30 或方差未知，其【均值 | 均值之差】是否为某一实数。

t-test 改进了 z-test 在样本量小于 30 时误差大的问题。

假设 $X$ 是正态分布的随机变量，其中样本为 $n$ ，均值是 $\mu$ ，方差是 $\sigma^2$ ，均未知。

样本均值为

$\overline{X}_n = \frac{\sum_i^n X_i}{n}$

样本方差 (Bessel-corrected) 为

$S_n = \frac{1}{n-1}\sum_i^n (X_i - \overline X)^2$

以下随机变量服从均值为 0 方差为 1 的正态分布

$\frac{\overline X_n - \mu_0}{\sigma / \sqrt n}$

单总体情况，t 统计量定义为

$t = \frac{\overline X_n - \mu_0}{S_n / \sqrt n}$

双总体情况，t 统计量定义为

$t = \frac{\overline X_1 - \overline X_2}{S_{\overline X_1 - \overline X_2}}$

应用1

给定样本：算法 A / B 流量下的用户付费情况

提出假设： $H_0$ 算法 B 与算法 A 人均付费一致

计算：样本的 $t$ 统计量 $t_0$ ；给定显著水平（置信度） $\alpha$ （如 95%），自由度 $N - 1$ （ $N$ 为样本数），查表得到 $t_1$ 。

结论：如果 $t_0 >> t_1$ ，我们有理由拒绝原假设。

应用2

For example, given a sample with a sample variance 2 and sample mean of 10, taken from a sample set of 11 (10 degrees of freedom), using the formula

$\overline X \pm t_{\alpha, n-1}\cdot \frac{S_n}{n}$

we can determine that at 90% confidence, we have a true mean lying below 10.58 and over 9.41.

In other words, on average, 80% of the times that upper and lower thresholds are calculated by this method, the true mean is both below the upper threshold and above the lower threshold. This is not the same thing as saying that there is an 80% probability that the true mean lies between a particular pair of upper and lower thresholds that have been calculated by this method.

应用3

import scipy.stats

print('1 t-test', scipy.stats.ttest_1samp([1.,0.9,1.1], popmean=1.0))
#Ttest_1sampResult(statistic=0.0, pvalue=1.0)

print('2 t-test', scipy.stats.ttest_ind([1.,1.2,1.1], [1,1.2,1.1], equal_var=True))
# Ttest_indResult(statistic=-0.8528028654224415, pvalue=0.4418233076836304)

最小样本数估算

二项分布 p 的置信区间

对二项分布 $X\sim B(\mu=p,\sigma=p(1-p))$ ，

$p'-z \sqrt{\frac{p'(1-p')}{n'}}\le p\le p'+z \sqrt{\frac{p'(1-p')}{n'}}$

其中 $n'=n+4,p'=\frac{X+2}{n}$ 对于 95% 显著水平或置信度， $z = 1.96$ 。

二项分布假设检验

TODO http://pages.stat.wisc.edu/~st571-1/10-power-4.pdf

应用1：双样本最小样本计算

样本1 转化率 1%，样本2 转化率 1.5%，sig.level 为 $\alpha=0.05$ ，power 为 $1-\beta=0.95$ ，求最小样本量

power.prop.test(n=NULL, p1=0.01, p2=0.015, sig.level=0.05, power=0.95, alternative = "two")
#     Two-sample comparison of proportions power calculation
#              n = 12829.31
#             p1 = 0.01
#             p2 = 0.015
#      sig.level = 0.05
#          power = 0.9
#    alternative = two.sided

应用2：单样本最小样本计算

样本1 转化率 1%，sig.level 为 $\alpha=0.05$ ，power 为 $1-\beta=0.95$ ，求最小样本量

install.packages('pwr')
library(pwr)
pwr.p.test(h=0.01,power=0.95,sig.level=0.05,alternative="two.sided")
#     proportion power calculation for binomial distribution (arcsine transformation)
#              h = 0.01
#              n = 129947.1
#      sig.level = 0.05
#          power = 0.95
#    alternative = two.sided

应用3：在线计算器

https://www.stat.ubc.ca/~rollin/stats/ssize/b1.html

原假设 H0：希望推翻的假设

备选假设 H1：希望验证的假设

判断\实际	没区别 H0	有区别 H1
有区别	$\alpha$ 一类错误, Sig. Level	$1-\beta$ Statisic Power
没区别	$1-\alpha$	$\beta$ 二类错误

Statistical Power （ $1 -\beta$ ）统计学功效：在假设检验中，拒绝原假设后，接受正确的替换假设的概率。在假设检验中有 $\alpha$ 错误和 $\beta$ 错误。 $\alpha$ 错误是 FP 错误， $\beta$ 错误是 FN 错误。

Significiant Level 显著性水平 $\alpha$ 。同时也是 Type I Error 出现的概率，FP，第一类错误意味着新的产品对业务其实没有提升，我们却错误的认为有提升。

Minimum Detectable Effect 最小改善程度 $\delta = (t_{\alpha/2} + t_{\beta} \sigma \sqrt{2/n})$

样本方差 $\sigma^2$ ，在二项分布中 $\sigma^2 = p \times (1 - p)$

求实验组的最小样本

$n \approx 16 \frac{\sigma^2}{\delta^2}$

https://jeffshow.com/caculate-abtest-required-sample-size.html#more-1798

https://www.cnstat.org/samplesize/11/

http://www.evanmiller.org/how-not-to-run-an-ab-test.html

http://www.evanmiller.org/ab-testing/sample-size.html

https://zhuanlan.zhihu.com/p/40919260

Two-porportion

TODO 公式推导 https://select-statistics.co.uk/calculators/sample-size-calculator-two-proportions/

P-value

p 值是指在一个概率模型中，统计摘要（如两组样本均值差）与实际观测数据相同，或甚至更大这一事件发生的概率[1] 。换言之，是检验假设 H0成立或表现更严重的可能性。p值若与选定显著性水平（0.05或0.01）相比更小，则H0会被否定而不可接受。然而这并不直接表明原假设正确。通常在H0设下，p值是一个服从[0,1]区间均匀分布的随机变量，在实际使用中因样本等各种因素存在不确定性。产生的结果可能会带来争议。

效应量

在统计学中，效应值（effect size，或译效果量）是量化现象强度的数值。[1]效应值实际的统计量包括了二个变数间的相关程度、回归模型中的回归系数、不同处理间平均值的差异……等等。无论哪种效应值，其绝对值越大表示效应越强，也就是现象越明显。效应值与特效检验的概念是互补的。在估算统计检定力、需要的样本数与进行元分析时，效应值经常扮演重要角色。

在研究结果中报导效应值被视为洽当的或必须的。[2][3]相对于统计学上的显著性，效应值有利于了解研究结果的强度。[4]特别是在社会科学和医学研究上，效应值更显得重要。绝对与相对效应值可以传递不同的讯息，又可互相补充讯息。

Effect size	d[5]	r[6]
较小	0.2	0.10
中等	0.5	0.30
较大	0.8	0.50

参数估计：正态总体

假设：已知样本 $x_1,...,x_n$ 来自正态分布总体 $X\text{~}N(\mu,\sigma^2)$ ，参数 $\mu, \sigma^2$ 未知。

参数估计：

点估计（矩法 / 极大似然法）：求得参数
区间估计：求置信系数为 p 的参数区间

例子：工厂生产零件的长度 X 服从正态分布 $N(\mu, \sigma^2=0.04)$ ，随机抽取 6 个样本，长度为 [14.6, 15.1, 14.9, 15.2, 15.1]，求置信系数为 0.95 的零件长度区间估计、方差区间估计

import scipy.stats
import numpy as np
mean = np.mean([14.6, 15.1, 14.9, 15.2, 15.1])
std = 0.2
print(scipy.stats.norm.interval(0.95,mean,std))
# (14.56, 15.39)

参考

样本容量估计梁雪枫 https://rstudio-pubs-static.s3.amazonaws.com/153235_a0277930a4924e46af765f4bbba3cdd6.html#exact-tests-for-proportions

https://www.zhihu.com/question/309884517

$t_{\alpha,n-1}$

t-统计量表

$Z_{\alpha/2}$

https://www.statisticshowto.datasciencecentral.com/z-alpha2-za2/

pCTR

Posted on 2019-05-29

Q 分布

Q 分布图：横轴 realCTR 纵轴 pCTR

保序：Q分布图是直线，样本排序正确

保距：45度，样本等距

评估指标

AUC

如果不考虑校准，AUC 是不错的指标。在生产环节，我们希望 pCTR 更接近实际 CTR，而非仅仅给出正确的 ranking order，避免 under-delivery 或者 over-dilivery。

NE

Normalized Entropy / Normalized CrossEntropy / Normalized Logarithmic
Loss，用样本 CTR 的交叉熵归一化 pCTR 的交叉熵。当 background CTR 越接近 0 和 1 时交叉熵会更好，加上分母使得 NE 指标不受 background CTR 影响

$NE = \frac{-\frac{1}{N}\sum_{i=1}^n(\frac{1+y_i}{2}\log(p_i) + \frac{1-y_i}{2}\log(1-p_i))}{-(p \log(p) + (1-p)\log(1-p))}$

其中 $y_i \in \{-1,1\}$ 是标签， $p_i$ 是预测值， $p$ 是经验 CTR。

Calibration

calibration = average estimated CTR / empirical CTR

负例子降采样

![image-20190529194656002](/Users/david/Library/Application Support/typora-user-images/image-20190529194656002.png)

Re-Calibration

等比推算

$q = \frac{p}{p + (1-p) / w}$

其中 q 是校准后的预测值，p 是降采样后的模型预测值，w 是负样本降采样率

推导方法：正样本数 a，负样本数 b，正样本采样率 l，负样本采样率 m，有

\begin{align} p&=\frac{a}{a+b}\\ q&=\frac{la}{la+mb}=\frac{a}{a+wb}\\ w&=\frac{l}{m} \end{align}

Isotonic fit （保序回归）

https://scikit-learn.org/stable/modules/calibration.html

https://scikit-learn.org/stable/modules/classes.html#module-sklearn.isotonic

Facebook 在线模型

![image-20190529201559938](/Users/david/Library/Application Support/typora-user-images/image-20190529201559938.png)

TEG 推荐架构

![image-20190530170232241](/Users/david/Library/Application Support/typora-user-images/image-20190530170232241.png)

参考

Practical Lessons from Predicting Clicks on Ads at
Facebook

CTR预估四: LR Bias和Q分布

MLR笔记

FTLR 总结

deep-ctr-models

Posted on 2019-04-25

常见的 CTR 预估模型有：

LR / 决策树系列
Embedding + 低阶交叉 + MLP：FM / DeepFM / NFM / FNN 系列
Embedding + 高阶交叉 + MLP：W&D / DCN / xDeepFM 系列
Attention：RNN CTR / DIN / DIIN / DIEN / CrossMedia / AutoInt（Multi-head Self-attention）
多任务联合建模： ESMM / ESM^2 / DUPN
双塔模型 DSSM 系列

深度 CTR 预估模型有：

Wide&Deep 16 兼具泛化性和记忆性的联合优化，cross product 进行特征交叉
DCN 17 使用 CrossNet 拟合任意高阶元素级交互（bit-wise 、上 1 层）
DeepFM 17 使用 FM 拟合 emb 向量的二阶交互
- NFM 17 在 FM 层后增加了 Bi-Interaction Layer 完成池化和特征交叉、增加 Dense 层
- AFM 17 在 NFM 结构增加 attention 机制学习交互特征的权重
- xDeepFM 18 使用 CIN 进行向量级别、高阶元素的交叉（vector-wise、上 n 层）
FNN 07 用 FM 预训练 emb 向量 + Dense 结构
- CCPM
- PNN SNN
- FGCNN
  
  FiBiNet 19 结合特征重要性和双线性特征交互
YouTubeDNN 16 通过 pooling 引入用户历史行为序列
- DIN 通过 attention pooling 引入带权重的用户历史行为序列
- DIIN 在 DIN 基础上增加图片特征
  - DIEN 19 引入 GRU 和辅助 loss 对用户兴趣演化建模
  - DSIN 19 基于用户行为序列同构 / 异构差异的建模
  - DSTN 19 引入上下文展示广告和历史点击、为点击广告辅助预测
  - MIMN 19 超长历史行为序列建模
  - ESMM 18 通过 pCTR pCVR 联合模型共享权制，多任务学习，解决转化样本有偏、稀疏问题
  - ESM^2 18 增加加购、收藏等多目标
  - DMIN 20 对用户行为切分 Session，使用自注意力建模 Session 的兴趣
AutoInt 19 引入 Transformer 中的 multi-head attention 机制
BST 19 引入用户行为序列 + Transformer

XGB

优化瓶颈

树型结构导致无法增量训练（FTRL）
稀疏的类别特征无法有效学习，onehot 后增加计算开销，且每个分类上数据量小（LR 记忆性）
特征交叉能力有限

GBDT + LR

Facebook ADKDD 2014

GBDT 叶子结点作为 LR 输入，通过 GBDT 做特征组合引入非线性。

FM

DeepFM

Huawei 2016

为了同时利用low-order和high-order特征，DeepFM包含FM和DNN两部分，两部分共享输入特征。对于特征i，标量wi是其1阶特征的权重，该特征和其他特征的交互影响用隐向量Vi来表示。Vi输入到FM模型获得特征的2阶表示，输入到DNN模型得到high-order高阶特征。模型联合训练，结果可表示为：

Wide&Deep

Google DLRS 2016

Wide：向量点积特征，具有记忆性。缺点：需要特征工程，不能覆盖未见的 query-item 特征，泛化差。

Deep：引入低维的 embedding，对未见的 query - item 具有泛化性。注意当 query - item 矩阵是稀疏且高秩时（如每个用户的兴趣很窄且小众），较难学习 embedding，出现过度泛化现象。此时需要 Wide 的记忆性来缓解。

训练：joint training 而不是 ensemble。相对而言，joint training 对子模型需要更少的模型容量 / 参数。Deep 泛化部分的不足，仅仅需要少量的 Wide 来弥补。Wide 用 FTRL，Deep 用 AdaGrad。其中 wide 部分类似 ResNet 的 residual shortcut。

工程：共使用 500 Bi 样本。对新样本，增量训练。上线前两个模型预测结果对比，做健全性检验（sanity-check）。

推理公式：

$P(Y=1|\mathbb{x})=\sigma (\mathbb{w}^T_{wide}[\mathbb{x},\phi(\mathbb{x})]+\mathbb{w}^T_{deep}a(l_f)+b)$

其中 $\sigma$ 是 sigmoid 函数， $[\cdot,\cdot ]$ 表示特征拼接。

向量点积：

$\begin{aligned} \phi_k(\mathbb{x})=\prod_{i=1}^d x_i^{c_{ki}}\\ c_{ki}\in \{0,1\}, \mathbb{x} = [x_1,x_2,...,x_d] \end{aligned}$

其中 $x_i$ 是某个特征， $c_{ki}$ 如果为 1 表示 $x_i$ 是 $\phi_k$ 变换的一部分。

向量点击可以进行特征组合，引入非线性，如 AND(gender=female, language=en) 这个特征，当且仅当这个用户的性别为 female，语言为 en 的时候，这个特征值才为 1，其他情况都为 0。

DCN 17’

http://xudongyang.coding.me/dcn/

ADKDD 17’ PDF，类似于Wide & Deep Network(WDL)，是用复杂网络预估CTR的一种方法。

与 DeepFM 相比，可以自动高阶特征：

通过设置交叉网络深度，能够限定交叉阶数
每层交叉时，做第零层与第一层的交叉 & 学习残差

其中每个 cross layer，通过学习函数 f 拟合层间残差

论文在 movielen 数据集上，与 LR FM DNN DeepCrossing 做对比。没有与 W&D 做对比的原因是 W&D 需要领域知识进行特征工程。没有与 DeepFM 对比，是同时期工作。

FNN & SNN & PNN

Feedforward Neural Network, ANN 2007

FM 预训练 emb 向量 + DNN 结构，无 embedding

Self-Normalizing Neural Network, NIPS 2017

Product-based Neural Networks, ICDM 2016

PNN 的 Embedding 和 Hiden Layer 1之间进行一次 inner / outer production，效果不错但增加了全连接规模导致训练较慢。

NFM 17’

Neral Factorization Machine, arxiv 2017 PDF

基于 FM 改进，在 FM 层后增加了 Dense 层 NFM与AFM用于CTR预估

与 YoutubeDNN 的 AVG Pooling 不同，NFM 通过 Bi-Interaction Pooling 完成池化和特征交叉：

$f_{BI}(V_x)=\sum_{i=1}^{n} \sum_{j=i+1}^{n} x_i v_i \odot x_j v_j$

其中 $x_i$ 是第 i 维特征， $v_i$ 是对应 embedding 矩阵， $\odot$ 是 element-wise product (outer product)。

实现代码：

https://github.com/nzc/dnn_ctr/blob/master/model/NFM.py

https://github.com/lambdaji/tf_repos/blob/master/deep_ctr/Model_pipeline/NFM.py

with tf.variable_scope("BiInter-part"):
    embeddings = tf.nn.embedding_lookup(Feat_Emb, feat_ids)         # None * F * K
    feat_vals = tf.reshape(feat_vals, shape=[-1, field_size, 1])
    embeddings = tf.multiply(embeddings, feat_vals)                 # vij * xi
    sum_square_emb = tf.square(tf.reduce_sum(embeddings,1))
    square_sum_emb = tf.reduce_sum(tf.square(embeddings),1)
    deep_inputs = 0.5*tf.subtract(sum_square_emb, square_sum_emb)   # None * K
    # DeepFM 没有 subtract 计算，是主要区别

论文在 MovieLen 数据集合与 WDL DCN 模型做对比。

NFFM 18’

NFM 的变种，在 Bi-Interaction 中将 FM 替换为 FFM

实现 https://github.com/guoday/ctrNet-tool/blob/master/models/nffm.py

腾讯 2018 Lookalike 第七名实现 https://github.com/guoday/Tencent2018_Lookalike_Rank7th

腾讯 2019 广告比赛预赛第一名实现 https://github.com/guoday/Tencent2019_Preliminary_Rank1st

AFM 17’

Attentional FM, arxiv 2017 PDF, 浙江大学 Jun Xiao et. al.

https://zhuanlan.zhihu.com/p/38517948

NFM 的改进，增加 attention 机制（pair-wise interaction + attention-based pooling），学习交叉相的权重，对无用的交叉项降权，减少噪声；同时可做重要性分析。

训练：先冻结 attension net 训练 FM embedding；然后固定 FM embedding 训练 attention net。

实现代码：

https://github.com/lambdaji/tf_repos/blob/master/deep_ctr/Model_pipeline/AFM.py

with tf.variable_scope("Pairwise-Interaction-Layer"):
    embeddings = tf.nn.embedding_lookup(Feat_Emb, feat_ids) # None * F * K
    feat_vals = tf.reshape(feat_vals, shape=[-1, field_size, 1])
    embeddings = tf.multiply(embeddings, feat_vals) #vij*xi

    num_interactions = field_size*(field_size-1)/2
    element_wise_product_list = []
    for i in range(0, field_size):
        for j in range(i+1, field_size):
            element_wise_product_list.append(tf.multiply(embeddings[:,i,:], embeddings[:,j,:]))
    element_wise_product = tf.stack(element_wise_product_list) # (F*(F-1)) * None * K
    element_wise_product = tf.transpose(element_wise_product, perm=[1,0,2])	# None * (F*(F-1)) * K

with tf.variable_scope("Attention-part"):
    deep_inputs = tf.reshape(element_wise_product, shape=[-1, embedding_size]) # (None * (F*(F-1))) * K
    for i in range(len(layers)):
        deep_inputs = tf.contrib.layers.fully_connected(inputs=deep_inputs, num_outputs=layers[i], weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg), scope='mlp%d' % i)

    aij = tf.contrib.layers.fully_connected(inputs=deep_inputs, num_outputs=1, activation_fn=tf.identity, weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg), scope='attention_out')# (None * (F*(F-1))) * 1

    aij_softmax = tf.nn.softmax(tf.reshape(aij, shape=[-1, num_interactions, 1]), dim=1, name='attention_soft')
    if mode == tf.estimator.ModeKeys.TRAIN:
        aij_softmax = tf.nn.dropout(aij_softmax, keep_prob=dropout[0])

with tf.variable_scope("Attention-based-Pooling"):
    y_emb = tf.reduce_sum(tf.multiply(aij_softmax, element_wise_product), 1) # None * K
    if mode == tf.estimator.ModeKeys.TRAIN:
        y_emb = tf.nn.dropout(y_emb, keep_prob=dropout[1])

    y_d = tf.contrib.layers.fully_connected(inputs=y_emb, num_outputs=1, activation_fn=tf.identity, weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg), scope='deep_out') # None * 1
    y_deep = tf.reshape(y_d,shape=[-1])

with tf.variable_scope("AFM-out"):
    y_bias = Global_Bias * tf.ones_like(y_deep, dtype=tf.float32)   # None * 1
    y = y_bias + y_linear + y_deep
    pred = tf.sigmoid(y)

论文在 MovieLens 数据集与 libFM / HOFM / Wide&Deep / DeepCross 算法对比，取得 SOTA 成绩。

DeepFM 17’

Huawei ICJA 2017

输入是高维、稀疏的、连续值离散值混合。

对比 FNN PNN W&D 网络结构

实现代码（省略 Dropout 和 BN）

https://github.com/lambdaji/tf_repos/blob/master/deep_ctr/Model_pipeline/DeepFM.py

with tf.variable_scope("First-order"):
    feat_wgts = tf.nn.embedding_lookup(FM_W, feat_ids)              # None * F * 1
    y_w = tf.reduce_sum(tf.multiply(feat_wgts, feat_vals),1)

with tf.variable_scope("Second-order"):
    embeddings = tf.nn.embedding_lookup(FM_V, feat_ids)             # None * F * K
    feat_vals = tf.reshape(feat_vals, shape=[-1, field_size, 1])
    embeddings = tf.multiply(embeddings, feat_vals)                 #vij*xi
    sum_square = tf.square(tf.reduce_sum(embeddings,1))
    square_sum = tf.reduce_sum(tf.square(embeddings),1)
    y_v = 0.5*tf.reduce_sum(tf.subtract(sum_square, square_sum),1)	# None * 1

with tf.variable_scope("Deep-part"):
    deep_inputs = tf.reshape(embeddings,shape=[-1,field_size*embedding_size]) # None * (F*K)
    y_deep = tf.contrib.layers.fully_connected(inputs=deep_inputs, num_outputs=1, activation_fn=tf.identity, weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg), scope='deep_out')
    y_d = tf.reshape(y_deep,shape=[-1])

with tf.variable_scope("DeepFM-out"):
    y_bias = FM_B * tf.ones_like(y_d, dtype=tf.float32)      # None * 1
    y = y_bias + y_w + y_v + y_d
    pred = tf.sigmoid(y)

xDeepFM 18’

KDD18 https://arxiv.org/pdf/1803.05170.pdf

腾讯广告比赛 19’ 冠军方案 https://zhuanlan.zhihu.com/p/73062485

论文在 Criteo 数据集与 DeepFM WDL PNN DCN 做对比，是目前 AUC 最好的方法。

与 DCN 不同，DCN 在 cross 层进行 bit-wise 的有限高阶特征交叉，不区分 vector field 的概念；xDeepFM 在 CIN 层以 vector-size 进行有限高阶特征交叉。例如，Age Field对应嵌入向量<a1,b1,c1>，Occupation Field对应嵌入向量<a2,b2,c2>，在Cross层，a1,b1,c1,a2,b2,c2会拼接后直接作为输入，即它意识不到Field vector的概念。Cross 以嵌入向量中的单个bit为最细粒度，而FM是以向量为最细粒度学习相关性，即 vector-wise。xDeepFM的动机，正是将FM的vector-wise的思想引入Cross部分。

简而言之：xDeepFM 是实现 vector-wise、与上n层 的高阶特征交叉，DCN 每层是 bit-wise、与上一层 的高阶特征交叉。

https://zhuanlan.zhihu.com/p/57162373

其中 CIN 结构下图，其中

$X^0 \in \mathbb R^{m\times D}$ 是输入，由 m 个 field， D 维的 embbeding feature 组成。

$X^k$ 表示第 k 层的输出， $H_k$ 表示 k 层的 vector 个数， $\odot$ 表示 hadamard 乘积（逐元素乘）

$X^k_{h,*}=\sum_{i=1}^{H_{k-1}}\sum_{j=1}^m W_{i,j}^{k,h}(X_{i,*}^{k-1} \odot X_{j,*}^0 )\in \mathbb R^{1\times D},\text{ }1\le h \le H_k$

CIN与Cross的几个主要差异：

Cross是bit-wise的，而CIN 是vector-wise的；
在第 $l$ 层，Cross包含从 1 阶～ $l+1$ 阶的所有组合特征，而CIN只包含 $l+1$ 阶的组合特征。相应地，Cross在输出层输出全部结果，而CIN在每层都输出中间结果。

复杂度

假设CIN和DNN每层神经元/向量个数都为 $H$ ，网络深度为 $T$ 。那么CIN的参数空间复杂度为 $O(mTH^2)$ ，普通的DNN为 $O(mDH+TH^2)$ ，CIN的空间复杂度与输入维度 $D$ 无关，此外，如果有必要，CIN还可以对权重矩阵 $\bm{W}$ 进行 $L$ 阶矩阵分解从而能降低空间复杂度。

CIN的时间复杂度就不容乐观了，按照上面介绍的计算方式为 $O(mH^2DT)$ ，而DNN为 $O(mDH+TH^2)$ ，时间复杂度会是CIN的一个主要痛点。

https://zhuanlan.zhihu.com/p/57162373

双塔模型

DSMM 13’

是微软 2013 年发表的一个 query / doc 相似度计算模型，思想是将不同的对象映射到同一个语义空间中，利用语义空间中的距离计算相似度。

首先将 query 和 doc 转化成 embedding 向量 $x$ ，这里针对英文单词提出了 word hash 方法降低计算量（中文不适用）。

接着词向量 $x$ 输入 DNN，选取 tanh 作为激活函数，得到 semantic feature $y$ ；然后 query 和 doc 会进行一次 cos 相似度计算得到 $R(q,D_i)$ ，最后经过 softmax 得到 $P(D_i|Q)$ ，其中

$R(Q,D)=\cos (y_Q, y_D) =\frac{y_Q^T y_D}{||y_Q||||y_D||}$

$P(D|Q)=\frac{\exp (\gamma R(Q,D))}{\sum_{D'\in D} \exp(\gamma R(Q,D'))}$

损失函数

$L(w) = -\log \prod_{(Q,D^+)} P(D^+|Q)$

其中 $Q$ 是 query， $D^+$ 是点击 doc

DSSM

MultiView-DSSM

共享 item 参数

T-DSSM 16’

MV-DSSM 模型加入 user temporal feature，引入 attention 机制，学习用户的短期兴趣。

难点在于时序特征的设计和训练，使用前应权衡业务对时间序列预测的需求。

YoutubeNet 17

Youtube 在 Recsys 17 发表

相对于双塔结构，Youtube DNN 对物品 embedding、用户embedding 求平均然后 concat，用统一的（用户，物品）向量空间替代了原来的两个向量空间。

Entire Space Multi-Task Model 18’

阿里在 KDD18 提出，为了解决 CVR 预估中样本选择偏差和数据系数问题，提出在全局空间建模（通过 pCTCVR 和 pCTR 来优化 CVR）和特征 Transform 方法来解决。

损失函数定义

$L(\theta_{ctr},\theta_{cvr}) = \sum_{i=1}^N l(y_i, f(x_i, \theta_{ctr})) + \sum_{i=1}^N l(y_i \& z_i, f(x_i;\theta_{ctr}) \times f(x_i;\theta_{cvr}))$

美团 Multi-Task Model

广告预估场景中存在多个训练任务，比如CTR、CVR、交易额等。既考虑到多个任务之间的联系，又考虑到任务之间的差别，我们利用 Multi-Task Learning的思想，同时预估点击率、下单率，模型结构如下图所示：

DIN 18’

阿里 KDD 2018 《Deep Interest Network for Click-Through Rate Prediction》

特点

引入用户购-商品历史的 Attention 机制
dice 激活函数

对用户 - 广告有特征：

$V_u (A) = f(v_{a},e_1,e_2,...,e_H)=\sum_{j=1}^H a(e_j,v_a)e_j=\sum_{j=1}^Hw_j e_j$

其中 A 是广告， $V_u$ 是用户特征， $e_i$ 是用户-商品序列。

函数 $a$ 是 Activation Unit，把输入 $x_1,x_2,x_2-x_1$ 拼接，输入 FC 层，输出权重 $w_j$ 。

Activation unit 可以针对候选广告，对相关度较高的用户行为商品embedding，给出较高的权重，如下图所示：

https://www.infoq.cn/article/XA055tpFrprUy*0UBdCb

DIEN 19’

阿里 AAAI 2019 《Deep Interest Evolution Network》

引入循环网络（双层GRU），对用户历史事件序列建模，捕获用户兴趣演化
引入辅助 loss 帮助 GRU 学习

DMIN 20’

阿里 CIKM 2020 《Deep Multi-Interest Network for Click-through Rate Prediction》PDF

对用户行为切分 Session，使用自注意力建模 Session 的兴趣

https://mp.weixin.qq.com/s/Pn8kSSBuWq-6dULfDKQoSQ

TDM

CrossMedia 17’

a.k.a. Deep Image CTR Model

《Image Matters: Visually modeling user behaviors using Advanced Model Server CIKM 2017》阿里 PDF

创新点：

将用户点击过的图像特征（与训练VGG的4096维输出）进行 attention pooling，对用户侧的视觉偏好建模（之前模型多用在物品侧）
AMS 架构解决计算瓶颈

RNN CTR 19’

KDD19 Click-Through Rate Prediction with the User Memory Network

http://www.semocean.com/tag/embedding/

AutoInt 19’

《Automatic Feature Interaction Learning 2019》 PDF

相比于 DCN 和 xDeepFM 采用交叉网络 + DNN 的双路结构，AutoInt 直接采用了单路的模型结构，将原始特征Embedding之后，直接采用多层 Interacting Layer进行学习（作者在论文的实验部分也列出了AutoInt + DNN 的双路模型结构：AutoInt+）；借鉴了NLP模型中 Transformer的 Multi-head self-attention 机制，给模型的交叉特征引入了可解释性。

以上是 single-head self-attention 结构，multi-head 由多个以上结构派生。

其中：

\begin{align} \alpha_{m,k}^{(h)} &= \frac{\exp(\psi^{(h)}(e_m,e_k))}{\sum_{l=1}^M \exp(\psi^{(h)}(e_m,e_l))} \\ \psi^{(h)}(e_m, e_k) &= \\ \hat{e}_{m}^{(h)} &= \sum_{k=1}^{M} \alpha_{m,k}^{(h)} (W_{Value}^{(h)}e_k) \end{align}

其中 $e_m \in \mathbb{R}^{d \times 1}$ 是 emb 向量， $W_{Query}, W_{Key}e_m \in \mathbb{R}^{d' \times d}$ 把输入emb 向量 d 维空间映射到 d’ 维空间。

对每个输入向量 $e_m$ ，每个 single-head 输出，是 Query 和 Keyword 向量的加权和。

对每个输入向量 $e_m$ ，多个 single-head 输出，拼接得到 multi-head 的 $\hat{e}_m$ ：

$\hat{e}_m=\hat{e}_m^{(1)} \oplus \hat{e}_m^{(1)} \oplus ... \oplus \hat{e}_m^{(H)}$

加上恒残差连接加速训练：

$e_m^{Res} = ReLU(\hat{e}_m + W_{Res}e_m)$

其中 $W_{Res} \in \mathbb{R}^{d'H\times d}$ 是投影矩阵，确保维度匹配。

把有输入向量的 multi-head res 输出向量 $e_m^{Res}$ 拼接起来，得到输出层：

$\hat{y} = \sigma\big( w^T(e_1^{Res} \oplus e_2^{Res} \oplus ... \oplus e_M^{Res}) + b \big)$

DSTN 19’

《Deep Spatio-Temporal neural Networks SIGKDD19》 PDF 阿里营销平台

b 模型，在 DNN 基础上，引入辅助广告特征：空域 — 同页的上下文广告；时域 — 最近点击未点击的广告。

c 模型，将目标广告的 embedding 和辅助广告一起输入到 attention 结构中，产生权重 pooling 起来，学习目标广告于辅助广告的重要性交互。

BST 19’

《Behavior Sequence Transformer for E-commerce Recommendation in Alibaba 19》 PDF 阿里搜索推荐组

问题：DIN 没有捕捉用户行为的连续性。

通过 Transformer Layer（仅 Encoding 部分），学习用户行为序列 item 与候选 item 的特征表达，输入三层 MLP学习特征的交互，最后输入 sigmoid 输出概率。

注：Transformer 来自《Attention Is All You Need》，抛弃传统 NLP 任务的 RNN 和 CNN 结构，通过 Attention + MLP 结构完成 encoder decoder 任务，并且融合了位置信息。

注：item 输入特征中，蓝色是物品特征（只需取 item_id 和 category_id）；红色是位置特征，模型学习位置编码（Positional Embedding）。

数据集合特点：用户行为丰富，淘宝 7 天数据，3亿用户，1千万物品，400亿样本，

效果：AUC 微小提升，CTR 显著提升

UMM

《Click-Through Rate Prediction with the User Memory Network DLP-KDD19》PDF git 阿里营销平台

DeepMCP

《Representation Learning-Assisted Click-Through Rate Prediction IJCAI19》PDF 阿里营销平台

传统的 DNN 模型将特征 embedding 用全连接网络往上送，最终和 label 一起计算 loss 并优化，学习时更多地关注 label 和特征之间的相互关系，虽然也有神经元连接起到交叉作用，但是特征和特征之间的相互影响学习的较少。比如某个用户点了某个 item，模型学习的结果并不要求用户和 item 表达有相似性。目前有些可借鉴的网络结构，如 DSSM，会要求两个输入 item 有一定的相似性。因此我们借鉴了这种思路，并将现有的模型结构融合起来，使得 DNN 网络学习的同时，对 Embedding 的学习也使用一些辅助网络来强化。对应到我们的业务中，如用户和广告，如果有点击关系，是否能相似一些，用户点击序列中的广告，是否能学的相似一些。

整个 DeepMCP 网络分为三个部分：一个是主网络，可以是任何的 DNN 网络结构，如 wide&deep，DeepFM；两个辅助网络：匹配子网络和关联子网络。匹配子网络学习的是用户和广告的相关性 ( 类似 DSSM )，关联子网络是学习广告和广告的相关性 ( 类似 word2vec 和 graph embedding )，目标是希望整个网络既有好的预测能力，又有好的 feature embedding 表达能力，从而提升模型的泛化能力。MCP 模型还有一个优点，线上 inference 时，只需要把主网络激活就可以了，其它部分不需要计算，对线上计算性能没有影响。

《深度时空网络、记忆网络与特征表达学习在 CTR 预估中的应用》秀武阿里高级算法专家

UIC&MIMN 19

《Practice on Long Sequential User Behavior Modeling for Click-Through Rate Prediction》PDF

MIMN借鉴了memory network的思想，用一个固定的memory矩阵对用户的兴趣信息进行存储。对于用户每一个新增的行为进行兴趣的encode后，写入其对应的memory slot中。在线计算某个用户CTR的时候使用当前最新的用户兴趣矩阵信息，在进行CTR的推断。这样的做法将长期兴趣建模和CTR预估两部分进行解耦，用户兴趣矩阵提前计算完毕，不会在对CTR预估计算带来latency瓶颈，同时在线需要通信和存储的内容也从原始行为序列变成了固定大小的memory矩阵。在这样的设计帮助下，我们实现了对1000量级的行为序列进行建模，并落地到了在线生产环境。但是这样的方案设计其实存在一些问题，其系统上带来的技术债暂且不表，算法上在目前的技术水平下存在一定的局限性。一个固定大小的memory 矩阵表达信息是有限的，如果我们想建模更长的用户行为序列，比如10000+，memory-based的方法会面临表达能力有限，难以过滤噪声，建模随时间信息遗忘的问题。UIC&MIMN解耦了兴趣建模和在线CTR预估的计算，建模用户兴趣时模型无法获取和使用待预估的候选item的信息。

SIM 20

《Search-based User Interest Modeling with Lifelong Sequential Behavior Data for Click-Through Rate Prediction》KDD19 阿里 PDF

《Life-long兴趣建模视角CTR预估模型：Search-based Interest Model》周国睿知乎

SIM 旨在研发一个可以根据预估目标item信息对用户全生命周期行为进行search，获取该item相关信息的方法。稳重提出了两阶段的search模式：general search 和 exact search。从精度角度我们将搜索拆解为一个相对粗糙普适的搜索和一个更为具体精确的搜索。

SIM 给出了一个通用的 framwork 让我们可以给每个用户的所有行为都构建一个索引，在预估CTR的时候可以充分的考虑用户的所有行为表达。

多任务学习

ESMM 18’

pCTR pCTCVR 任务辅助 pCVR 学习，缓解 pCVR 样本选择有偏（SSB）、数据稀疏（DS）的问题。

所有 user / item embedding lookup 结果，会 element-wise 加起来，再进行 concat，这样的设计利于特征扩展。

损失函数

$L(w_{ctr},w_{cvr})=\sum_i L(y, f(x_i, w_{ctr})) + \sum_i L(y_i\&z_i, f(x_i;w_{ctr}) *f(x_i;w_{cvr}))$

Oversampling：把正样本复制多分，缓解 DS 问题；

AMAN：把 All Missing As Negative，通过引入未点击未转化样本，部分解决 SSB 问题；

UNBIAS：

DIVISION：

ESM^2

《Entire Space Multi-Task Modeling via Post-Click Behavior Decomposition for Conversion Rate Prediction》Ali arxiv2019 PDF

更多任务

MoSE 20’

《Multitask Mixture of Sequential Experts for User Activity Streams》Google KDD2020 PDF 深度传送门

本文主要研究了如何在多任务学习场景中针对用户行为序列进行建模，提出了一套新颖的模型框架 MoSE（Mixture of Sequential Experts）。在当前最新的MMoE多任务学习框架中使用LSTM针对用户行为序列进行显式建模。同时，本文也通过离线实验以及GMail的线上实验证明了本文的有效性。

MMoE 18’

《Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts KDD18》PDF

多任务学习常见结构：share-bottom 共用隐层，参数少，避免过拟合，但子任务差异很大效果不佳。

论文提出 MMoE 结构，通过 multi gates 和 mult experts，学习每类任务的表达，解决 shared-bottom 子任务差异大效果不佳的问题。

与 ESMM 不同，子任务之间无关联。

SNR 19’

《SNR: Sub-Network Routing for Flexible Parameter Sharing in Multi-task Learning AAAI19》PDF

解决多任务学习问题，任务间相关性低时，shared-bottom 或 MMoE 等方法精度不高的问题。

YouTube Multitask Ranking System

《Recommending What Video to Watch Next: A Multitask Ranking System RecSys19》 PDF

解决：

MMoE 视频推荐中的多任务目标：比如不仅需要预测用户是否会观看外，还希望去预测用户对于视频的评分，是否会关注该视频的上传者，否会分享到社交平台等。
Shallow Tower 预测偏置位置信息，输入 pCTR 任务：比如用户是否会点击和观看某个视频，并不一定是因为他喜欢，可能仅仅是因为它排在推荐页的最前面，这会导致训练数据产生位置偏置的问题。

PFD 20’

《Privileged Features Distillation at Taobao Recommendations KDD20》 PDF

损失函数

$\min_{W_s,W_t}(1-\lambda) L_s(y, f_s(X;W_s)) + \lambda L_d(f_t(X^*,X;W_t), f_s(X;W_s)) + L_t(y, f_t(X^*,X;W_t))$

其中 $L$ 是 student、teacher 模型原始 loss， $f$ 是 student、teacher 模型的预估值。 $X^*$ 是普通特征+优势特征， $X$ 是普通特征。

蒸馏方法通常训练老师，再固定老师权重训练学生；为加速，两个模型同时训练，通过调整 $\lambda=0$ 先重点训练 teacher 模型，再逐渐增加 $\lambda$ 权重。

淘宝推荐系统架构

统一蒸馏：MD（模型蒸馏）与 PFD（优势特征蒸馏）结合，用精排 CTR 模型做老师，粗排模型做学生

UW Loss 18’

《Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics CVPR18》PDF

与固定权重损失 $L_{total}=\sum w_i L_i$ 相比，UW Loss 的权重是通过最小化损失函数学习得到的。

推导：令 $f^W(x)$ 为神经网络的输出值，定义概率模型（回归）

$p(y|f^W(x)) = N(f^W(x), \sigma^2)$

定义概率模型（分类）

$p(y|f^W(x)) = Softmax(f^W(x))$

定义多任务 likelihood

$p(y_1,...,y_K|f^W(x))=p(y_1|f^W(x)) ... p(y_K|f^W(x))$

回归模型的多任务 log likelihood （Gaussian likelihood，假设概率模型服从高斯分布）

$\log p(y_K|f^W(x)) \approx -\frac{1}{2 \sigma^2}|| y - f^W(x)||^2 - \log \sigma$

对两个回归任务，损失函数为

\begin{align} L(W,\sigma_1,\sigma_2) &=-\log p(y_1,y_2|f^W(x)) \\ &\approx \frac{1}{2\sigma_1^2}||y_1 - f^W(x)||^2 + \frac{1}{2\sigma_2^2}||y_2 - f^W(x)||^2 + \log \sigma_1 \sigma_2 \\ &= \frac{1}{2\sigma_1^2} L_1(W)+\frac{1}{2\sigma_2^2} L_2(W)+\log \sigma_1 \sigma_2 \end{align}

对比固定权重损失

$L_{total}=\sum w_i L_i$

帕累托最优

《A Pareto-Efficient Algorithm for Multiple Objective Optimization in E-Commerce Recommendation RecSys19》PDF

如何用模型自动寻找最优的目标权重参数组合，就是一个非常有价值的方向，目前最常用的方式是采用帕累托最优的方案来进行权重组合寻优，这是从经济学引入的技术方案，未来还有很大的发展空间。

多模态信息融合

加入 user / item 侧的音视频特征、图片特征。难点在于工程支撑，如何设计结构获取有效的特征表示。

《Collaborative Multi-modal deep learning for the personalized product retrieval in Facebook Marketplace》

《Image Matters: Visually modeling user behaviors using Advanced Model Server》

实现

https://github.com/guoday/ctrNet-tool (tensorflow layer API, criteo 数据集 dense 格式)

https://github.com/shenweichen/DeepCTR (tensorflow keras API)

https://github.com/nzc/dnn_ctr (pytorch)

https://github.com/lambdaji/tf_repos/tree/master/deep_ctr (tensorflow-1.12 Pyhton2.7 Estimator API，criteo 数据集 libsvm 格式，支持 TFServing 模型导出)

https://github.com/lambdaji/tf_repos/tree/master/DeepMTL (ESMM tensorflow-1.12 Pyhton2.7 Estimator API ESMM，天池数据集，支持 TFServing 模型导出)

Reference

https://zhuanlan.zhihu.com/p/40135103

fanding.xyz

深度学习在美团搜索广告排序的应用实践 https://tech.meituan.com/2018/06/07/searchads-dnn.html

远程监督 https://blog.csdn.net/m0_38031488/article/details/79852238

2019 腾讯广告冠军方案知乎

推荐系统中的注意力机制——阿里深度兴趣网络（DIN）知乎

semocean’s blog

阿里 XDL 算法解决方案

DeepCTR：易用可扩展的深度学习点击率预测算法包知乎

TODO

漫谈深度学习时代点击率预估技术进展朱小强 InfoQ

MLR 阿里妈妈算法团队

详解阿里之Deep Interest Evolution Network(AAAI 2019) 知乎

CTR预估模型发展过程与关系图谱知乎

NLP 中的 Transformer 和 BERT 知乎

贝叶斯定理

Posted on 2019-04-14

贝叶斯定理

由联合概率的乘法交换律得到

$\begin{aligned} P(H,D) &= P(D,H)\\ P(H)P(D|H) &= P(D)P(H|D)\\ P(H|D) &= \frac{P(H)P(D|H)}{P(D)}\\ P(H_i|D) &= \frac{P(H_i)P(D|H_i)}{\sum_i P(H_i)P(D|H_i)} \end{aligned}$

其中

$P(H)$ 为先验概率，即在得到新数据前的某一假设
$P(H|D)$ 为后验概率，即在看到新数据后，我们待求解的该假设的概率
$P(D|H)$ 称为似然度，是该假设下得到这一数据的概率
$P(D)$ 称为标准化常量，是在任何假设下得到这一数据的概率

将 $D$ 变成样本 $x$ ，将 $H$ 变成连续的参数 $\theta$ ，有贝叶斯公式

$\pi(\theta_i|x)=\frac{f(x|\theta_i)\pi(\theta_i)}{\int_\Theta f(x|\theta_i)\pi(\theta_i)}$

其中

$\pi(\theta)$ 为先验分布，可设为 0-1 均匀分布
$\pi(\theta|x)$ 为后验分布
$f(x|\theta)$ 为似然函数，即我们观测到的样本分布

累计分布函数 CDF $F_X(x)$ ，也叫分布函数，有 $F_X(x) = P(X \le x)$ ，是非降、有界、有连续的函数。

概率密度函数 PDF $f_X$ ，有 $F_X(x)=\int_{-\inf}^x f_X(t)dt$ ，是有界、单调、右连续的函数。

求解参数 $\theta$ ，可以用矩估计法或极大似然估计法

$\arg \max_{\theta} \text{MLE}(\theta)=\prod_i f(x_i | \theta)$

Xavier 初始化方法

Posted on 2019-03-21

Standard Init

$W \sim U[-\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}]$

其中 $n_i$ 是第 i 层的输入节点。

在 Xavier Init 提出前，一般用 unsupervised pre-trainning 和 greedy layer-wise procedure 来训练神经网络。

Xavier Init

$W \sim U[-\frac{\sqrt 6}{\sqrt{n_i + n_{i+1}}}, \frac{\sqrt 6}{\sqrt{n_i + n_{i+1}}}]$

其中 $n_i$ , $n_{i+1}$ 是第 i 层的输入、输出节点，以下是推导过程。

RTB 广告竞价策略

Posted on 2019-03-18

RTB 广告流程

竞价策略

广告主在收到竞价请求后，会根据竞价规则，一般是 CPM 或者 CPC，进行出价。

固定出价

对所有广告请求，出价为固定值。

随机出价

在一定范围内，随机出价。

受限 CPA 出价

$eCPM = pCTR \times pCVR \times 1000 \times CPA$

其中 CPM 是广告千次曝光价格，CPA 是每次转化成本，CTR 是广告转化率。对于每个竞价请

受限 CPC 出价

$eCPM = pCTR \times pCVR \times 1000 \times mCPC$

在 CPC 模式下，广告主会设定最高点击成本 mCPC，可用上述公式出价。

线性出价

$eCPM = a \times pCTR \times pCVR + b$

美团DSP竞价策略实战

非线性出价

《Optimal real-time bidding for display advertising SIGKDD14》PDF

《Optimal Real-Time Bidding Frameworks Discussion》PDF

$eCPM = \sqrt{\frac{\lambda}{c} \theta + c^2 } - c$

出价模型是预算有限的情况下最大化收益，优化目标为

$b()_{ORTB} =\arg \max_{b()} N_T \int_{x}\theta(x) w(b(\theta(x))) p_x(x) dx$

$s.t. N_T \int_{x} b(\theta(x)) w(b(\theta(x))) p_x(x) dx \le B$

其中假设某个广告在排期 $T$ 内总共符合其定向的广告请求共 $N_T$ 个，每个广告请求特征 $x$ ，满足定向条件的 $x$ 先验为 $p_x(x)$ 。给定收益函数 $\theta(x)$ ，如 pCTR，竞价函数 $b(\theta(x))$ ，竞价成功率函数 $w(b(\theta(x)))$ ，广告预算 $B$ 。

因为 $x$ 和 $\theta(x)$ 的关系是确定的，那么他们概率密度函数也是确定的

$p_\theta(\theta(\mathbb{x}))=\frac{p_x(\mathbb{x})}{||\nabla\theta(\mathbb{x})||}$

优化目标代入上式，有

$b()_{ORTB} ={\arg\max}_{b()} N_T \int_\theta\theta w(b(\theta))p_\theta(\theta)d\theta$

$s.t. N_T \int_\theta b(\theta)w(b(\theta))p_\theta(\theta)d\theta \le B$

拉格朗日目标函数为

$\mathcal{L}(b(\theta), \lambda) = \int_\theta \theta w(b(\theta))p_\theta(\theta)d\theta - \lambda \int_\theta b(\theta)w(b(\theta))p_\theta(\theta)d\theta + \frac{\lambda B}{N_T}$

其中 $\lambda$ 是拉格朗日乘子。

由变分法（calculus of variations）， $b(\theta)$ 的欧拉-拉格朗日条件为

$\theta p_\theta(\theta) \frac{\partial w(b(\theta))}{\partial b(\theta)} - \lambda p_\theta(\theta)\big[ w(b(\theta)) + b(\theta) \frac{\partial w(b(\theta))}{\partial b(\theta)} \big]=0$

$\lambda w(b(\theta)) = \big[\theta - \lambda b(\theta)\big]\frac{\partial w(b(\theta))}{\partial b(\theta)}$

根据 iPinYou 现实数据集，拟合出 $w$ 与 $b(\theta)$ 的函数关系，并求导

$w(b(\theta))=\frac{b(\theta)}{c+b(\theta)}$

$\frac{\partial w(b(\theta))}{\partial b(\theta)}=\frac{c}{c+b(\theta)^2}$

代入欧拉-拉格朗日条件公式，得到

$b_{ORTB1}(\theta)=\sqrt{\frac{c}{\lambda}\theta + c^2}-c$

PID 策略

对成本受限的 oCPC 竞价，引入 PID 调价因子 $\lambda$ ，改变出价：

$eCPM = 1000 \times pCTR \times (CPC + \lambda)$

间隔一小时，误差定义

$error_t = targetCPC_t - realCPC_t$

PID 公式

$\lambda_{t+1} = \lambda_t + K_p error_t + K_I \sum_i error_i + K_D (error_t - error_{t-1})$

其中 $K_P$ 为比例系数（当前误差情况）， $K_I$ 是积分系数（解决稳态误差，去误差累计）， $K_D$ 是微分系数（未来误差预测）。三者依靠经验值调整。

优点是泛化性好，缺点时无法对上下文特征利用不完全。

https://mp.weixin.qq.com/s/xX8eGjmQqeQptyX9KOtOwQ

强化学习免模型策略：DQN

《Budget Constrained Bidding by Model-free Reinforcement Learning in Display Advertising CIKM18》PDF

问题：二价竞得机制，目标最大化广告曝光，约束预算受限

MDP 建模，并提出强化学习模型求解。

赏函数设计：原有设计——一段时间内竞得数，即广告曝光数，为了增加奖赏，action 会降低 $\lambda$ 使得出价更激进，提前耗尽预算；新设计——增加预算限制建模，

参考问题：Resource-constrained RL Problems，如 Gold Miner 游戏

算法：Deep Reinforcement Learning to Bid

DQN 框架，维护 Q(s, a) 值函数，利用经验回放学习，其中 a 是出价系数 $\lambda$ ，s 是状态，r 由 RewardNet(s, a) 估算
adaptive $\epsilon$ -greedy 选择 action
RewardNet 通过经验回放估算 reward

MoTiAC

《MoTiAC: Multi-Objective Actor-Critics for Real-Time Bidding 2020》腾讯广告 PDF

《Reinforcement Learning with Sequential Information Clustering in Real-Time Bidding CIKM19》PDF

附录

约束最优化问题求解：拉格朗日乘子法

假设 $f(x), g_i(x), h_j(x)$ 是定义在 $\mathbb R^n$ 上的连续可微函数，定义不等式约束最优化问题为

$\begin{aligned} \min_{x\in\mathbb R^n}\ &f(x)\\ s.t.\ &g_i(x) \le 0 \\ &h_j(x) = 0 \end{aligned}$

引入拉格朗日乘子 $\alpha_i, \beta_i$ 且 $\alpha_i \ge 0$ ，定义拉格朗日函数为

$L(x,\alpha,\beta)=f(x)+\sum_i \alpha_i g_i(x) + \sum_j \beta_j h_j(x)$

K.K.T. 条件，即 $x$ 是函数 $L$ 的最优值必定满足下面条件

$\begin{aligned} \frac{\partial L}{\partial x} &= 0 \\ h(x) &= 0\\ g(x) &\le 0\\ \alpha_i g_i(x) &= 0\\ \alpha_i &\ge 0 \end{aligned}$

参考

http://tech.youmi.net/2016/06/158883267.html

http://wnzhang.net/papers/ortb-kdd.pdf

https://zhuanlan.zhihu.com/p/55798676

https://zhuanlan.zhihu.com/p/38163970

https://zhuanlan.zhihu.com/p/26514613

Lookalike 算法调研

Posted on 2018-09-11

https://zhuanlan.zhihu.com/p/37400021

难点

A 对目标直接建模 or 迁移学习：长期以 ROI 为目标，短期以 CPA 为目标

B 种子包：各式各样，训练二分类通过AUC评估，与目标不一致

如有条件，先试种子包，如成本在 KPI 下，再用扩散包

种子包注册改为点击转化用户

C 点击转化付费数据：有偏稀疏，广点通/信息流媒体未充分利用

点击 ieg_tdbank::o2_rt_dsl_mobile_click_ios_fdt0

回流 ieg_mms::mas_user_back_adv

D 转化数据延时反馈

E 对付费数据利用

F 对玩家-游戏图数据利用

尝试方向

用户感兴趣的游戏预测：用户-游戏图的边预测，应用《Link Prediction Based on GNN, NIPS18》 PDF /
游戏安装预测 App2Vec PDF 改进 CBOW 在 softmax 加入两个 app 使用间隔时长（考虑人均游戏较少问题）
NN 端到端方法：《Comprehensive Audience Expansion based on End-to-End Neural Prediction SIGIR19》 PDF 文中对一个用户多次 DSP 广告曝光 / 点击特征做归一化作为特征，是否购买作为标签（拿不到广点通曝光数据）；对比 PU learning 问题的三种采样方法 spy / pre-train / bootstrap；对比 LR / FM / bn_mlp / s_mlp / s_bn_mlp 模型，其中 s_mlp 效果最好
GNN 端到端方法：微信广告 GAT Lookalike Chrisyi 分享，基于共同朋友参与多的广告转化率高假设，微信好友扩散（考虑我们关系网较少）
NE 方法：用户-游戏异构图 MetaPath2vec 作为特征输入（基于相似度方法精度低，只用 NE 做为特征）
PU Learning：种子用户 Lookalike 基础上，持续加入曝光点击用户和未转化用户；利用多渠道曝光点击转化，持续扩散
RTB 优化：跳过 Lookalike，根据 eCPM ( pCVR x pCVR x 1000 x oCPA) 是否大于广告位最低价，决定是否竞价 / 增加 pLTV(user, game) 用于出价

Lookalike

Rule-based

常见于广告平台标签定向，选择年龄、性别、职业、兴趣标签，定向投放。

《Effective audience extension in online advertising SIGKDD15》PDF

Graph-based

《Link Prediction Based on GNN, NIPS18》 PDF 边缘预测：玩过哪些游戏的用户，更容易安装新游戏。

《App2Vec: Vector modeling of mobile apps and applications ASONAM16》 PDF 应用安装预测，改进 CBOW 在 softmax 加入两个 app 使用间隔时长

Similarity-based

UserCF / ItemCF / MF：协同过滤，挑战：数据高维稀疏

Graph Embedding: LINE / GES / Node2vec

YoutubeDNN 召回部分：根据用户观看搜索序列进行NE；把搜索观看视频 emb 作为 DNN 输入，预测观看时长，用 DNN 最后一层作为用户表达，召回距离相近的用户。

《Audience Expansion for Online Social Network Advertising KDD16》PDF LinkedIn 基于用户属性的相似度

《Score Look-Alike Audiences ICDM16》PDF Yahoo! 基于相似度的 LSH 方法：以广告主指标作为优化目标；未转化用户作为负样本；其中局部敏感哈希 LSH ，是一种使特征相近的用户哈希到相同桶的方法。

Regression-based

LR《A Sub-linear, Massive-scale Look-alike Audience Extension System BigMine16》 PDF Yahoo! 1. 构建 “用户-用户相似图” 缩小候选集；2. 针对每个 campaign，特征选择 + LR 模型打分

GBDT

RALM《Realtime Attention-based Look-alike Model KDD19》 PDF 将 lookalike 方法用于实时资讯推荐：通过某 item 的 seed user 计算候选 user 的 lookalike score，以决定是否推荐 item。系统分为两部分 1. 用户表示学习（右）； 2. Lookalike 学习（左）

数据特点：user-item 丰富，冷启动 item

MLP《Comprehensive Audience Expansion based on End-to-End Neural Prediction SIGIR19》 PDF 是基于 MLP 的端到端方法，对一个用户多次 DSP 广告曝光 / 点击特征做归一化作为特征，是否购买作为标签（拿不到广点通曝光数据）；对比 PU learning 问题的三种采样方法 spy / pre-train / bootstrap；对比 LR / FM / bn_mlp / s_mlp / s_bn_mlp 模型，其中 s_mlp 效果最好

半监督学习 - PU Learning

问题：给定正样本 P，未标记样本 U，训练二分类器

挑战：负样本不易获取、负样本多样性、负样本动态变化

综述对比

《A Survey on Postive and Unlabelled Learning》 PDF

《An Evaluation of Two-Step Techniques for Positive-Unlabeled Learning in Text Classification》 PDF

简单方法：把未标记样本 U 作为噪声很大的负样本来处理

两步方法

训练分类器 g，从未标记样本 U 中，寻找可靠负样本 RN
用 P 和 RN 组成数据集，训练分类器 f

第一步方法：计算可靠负样本

Rocchio

《Relevance feedback in information retrieval 1971》PDF

动机：选择文档向量表示 $\vec d$ 、相似度衡量函数 $f$ ，对每个 U 中的样本：把与 P 样本相似、与 U 不相似的样本，选入可靠负例 RN。

算法：每个文档 $\vec d$ 用 IR 分数如 TFIDF 表示； $C_j$ 是 $j$ 类文档集合， $c_j$ 是其 prototype vector，则

$\vec{c_j}=\alpha\frac{1}{|C_j|}\sum_{\vec d \in C_j}\frac{\vec d}{||\vec d||} - \beta \frac{1}{|D - C_j|} \sum_{\vec d\in |D - C_j|} \frac{\vec d}{||\vec d||}$

其中 $\alpha$ 、 $\beta$ 是文档集合 $|C_j|$ 、 $|D-C_j|$ 的权重。

测试时，一些相似度函数 f 可以衡量 $d$ 和 $c_j$ 的相似度，分数那高的那一类分配给文档 $d$ 。

Rocchio 算法为 P U 分别构建 prototype vector，选择 RN 样本依据：U 中样本与 negative prototype vector 有更高相似分数。

Cosine-Rocchio

计算 U 中，与 P 余弦相似度高的样本，作为潜在负样本 PN
应用 Rocchio 分类方法，构建分类器 g，对 P 和 PN 二分类
用 g 对 U 分类，判别负样本作为可靠负样本 RN

Spy

《Partially supervised classification of text documents ICML02》 PDF

P 全部正样本；U 未标记样本；S 正样本子集
构建数据集正样本 P - S 和负样本 U + S ，训练二分类器 g
对 S 应用 g 确定阈值 t；构建 RN （可靠负样本）
从 U 选取满足条件的样本 $g(u) > t$

1-DNF

《PEBL: positive example based learning for web page classification using SVM KDD02》PDF

选择正特征：对比相对 U，在 P 频率更高的特征（文本分类任务中，找词频高的词包）
选取 RN 可靠副样本：在 U 中找不包含正特征的样本

Naïve Bayesian

构建训练集 U 和 P，学习 NB 分类器
对 U 使用 NB 分类器，得到 RN 样本

第二步方法

SVM - based

构建分类器 f 学习 P RN 二分类
对 Q 应用 f，若样本判为负例则从 Q 移入 RN
重复直到收敛，取最终分类器作为结果

EM - Naïve Bayesian

Q (=U-RN) 视为未知类别
构建 NB 分类器 f，P 作为正例，RN 为负例
Expectation 步：f 对 Q 样本分类
Maximization 步：从 P RN Q 学习新的 f
迭代 EM 直至收敛，取最后一个分类器作为结果

https://zhuanlan.zhihu.com/p/37575364

模型加权方法

《Learning classifiers from only positive and unlabeled data SIGKDD08》PDF

融入先验类别（Incorporation of the Class Prior）：尝试给正样本P和未标记样本U赋予权重，并给出样本属于正标签的条件概率估计。

考虑样本 $<x, y, s>$ 服从分布 $p(x, y, s)$ ，只有 $<x,s>$ 记录在训练集合，其中 $s$ 是观察标签、 $y$ 是实际标签。

假设训练集正样本是从所有正样本随机采样得到，且与特征 $x$ 无关

$p(s=1|x,y=1)=p(s=1|y=1)=c$

首先训练分类器 $g(x)=p(s=1|x)$ 预测样本被观察为正 $s=1$ 的概率（给定实际标签为正 $y=1$ ）

$p(s=1|y=1)=\frac{1}{n_p} \sum_{x\in P} g(x)$

其中 $n_p$ 是正样本候选集 P 的势（cardinality）

接下来，对每个未标记样本，可以认为是正样本加权 $p(y=1|x,s=0)$ 和负样本加权 $1-p(y=1|x,s=0)$ 的集合。

其中正样本加权

$p(y=1|x,s=0)=\frac{1-p(s=1|y=1)}{p(s=1|y=1)}\frac{p(s=1|x)}{1-p(s=1|x)}$

至此，通用分类器可以在 $<x,s>$ 数据集和以上权重训练。代码实现

《Building Text Classifiers Using Positive and Unlabeled Examples ICDM03》DOC

《Towards Positive Unlabeled Learning for Parallel Data Mining: A Random Forest Framework ADMA14》 PDF

一种基于随机森林的 PU 学习方法

《Learning with confident examples: Rank pruning for robust classification with noisy labels UAI17》PDF

图像分类 PU-Learning 问题，Rank Pruning 方法，每次迭代从 U 移除最不可信样本

《Learning with a generative adversarial network from a positive unlabeled dataset for image classification ICIP18》PDF

问题：图像分类 PU-Learning。

效果：在 CIFAR-10 数据集本文 P-GAN 方法比 Rank Pruning 方法更好；在 MNIST 结果一般。（谨慎使用）

回顾 GAN 方法：G 为生成模型，生成假样本；D 为判别模型，判断是真样本和还是 G 生成的假样本。

损失函数：

\min_G \max_D V(D, G)=\mathbb{E}_{x_R\sim p_{data(x_R)}}[\log D(x_R)] \\ + \mathbb{E}_{z\sim p_z(z)}[\log(1-D(G(z)))]

其中 $x_F$ 是生成假样本， $x_R$ 是真实样本；z 是随机噪声， $G(z)$ 是从随机噪声生成的假样本。

当判别器 D 无法分辨真样本和 G 生成的假样本时，即 $y_D \rightarrow 0.5$ ，G 生成的假样本数据分布 $p_G(x_F)$ 接近真样本的数据分布 $p_{data}(x_r)$ ，即

p_G(x_F) \xrightarrow[y_D \rightarrow 0.5]{} p_{data}(x_R)

本文方法 Postive-GAN：

《On Positive-Unlabeled Classification in GAN CVPR20》 PDF

问题：针对以往的 Postive-Fake GAN 方法中，D 学习区分真假样本，而忽视部分样本质量逐渐提升、生成样本质量不平衡的问题（假样本中部分太真、部分太假）。

解决：提出 Postive-Unlabeld GAN，D 区分高质量假样本和低质量假样本，使得 G 能够改进低质量样本。

GAN 模型目标函数：

\min_G \max_D V(D, G)=\mathbb E_{x\sim p_{data}} [f_1(D(x))] \\ - \mathbb E_{z\sim p_z}(f_2(D(G(z))))

本文目标函数：

\min_G \max_D V(D, G)=\pi \mathbb E_{x\sim p_{data}} [f_1(D(x))] \\ + max\{0, \mathbb E_{z\sim p_z}(f_2(D(G(z))))\} \\ - \pi \mathbb E_{x\sim p_{data}} [f_2(D(x))]

其中 f1 分类为真的损失函数， $f2$ 是分类为假的损失函数，如交叉熵。

效果：STOA，对 LSUN CAT CelebA 等 64x64 数据集，G 能生成高质量假样本。本问方法可结合主流 GAN 框架使用，生成高质量的假样本。

《Training deep neural networks on noisy labels with bootstrapping ICLR15》 PDF

TODO

参考

node2vec

DNN for Yotube Recommendation

DSSM PDF

微信广告 Lookalike 易玲玲知乎

微信看一看 RALM 知乎

微博广告 Node2vec + DNN https://juejin.im/entry/59b0b5276fb9a024747f26ba

半监督学习知乎

PU Learning在风控中的应用（理论篇）知乎

Plato 平台介绍 KM

异构 Network Embedding（一）概述 KM

手把手教你在柏拉图跑 Network Embedding KM

推荐模型中的样本迁移问题 KM

半监督学习方法综述计算机学报

RTB

手动设置竞价（Manual）

老虎机 Bandit，action 影响回报

上下文老虎机（Contexual Bandit），action 和 contex 都影响回报知乎阿里小毛驴

Advantageous Actor-critic (AC A2C A3C) 知乎

连续动作控制（DDPG）

阿里：分布协同多智能体竞价系统（DCMAB）

KDD2012 Bid Optimizing and Inventory Scoring in Targeted Online Advertising 非线性竞价函数 PDF CN

参考

user embedding技术1：用户行为序列建模bert4userembedding

user embedding技术2: Bert 大规模预训练算法

user embedding技术3 – SocialTrans：BERT与GNN的结合

user embedding技术4：Graph Auto-encoder在微信社交网络上的实践

user embedding技术5：GraphSage在微信社交网络上的实践

当图神经网络遇上社交推荐 - PlatoDeep在微信朋友圈广告中应用 KM

GNN 算法框架及其应用概述 KM

量化交易笔记

Posted on 2018-09-10

衡量策略的指标

CNN 模型压缩方法

Posted on 2018-07-06

MobileNetV1

Google Howard 等人提出的适用于移动设备的，使用 depthwise separable conv 构建的轻量 CNN。

引入了两个全局超参数，能够有效地平衡了速度和准确率。超参数允许模型构建者根据他们的问题，选择模型大小。

Depthwise Seperable Conv

这种卷积用两层结构，替代了标准卷积，加速计算：

depthwise conv：一个 filter 只过滤一层 feature map（标准卷积是所有层）。
pointwise conv：1x1 卷积，输出结果到下一层。

depthwise conv

简单地说，depthwise conv 把标准卷积的求和步骤，放到了第二步 1x1 conv 来做。

标准卷积输入 $D_F \times D_F \times M$ 的特征 map，输出 $D_G \times D_G \times N$ 的 feature map，其中 M 是输入深度，N 是输出深度， $D_F,D_G$ 是输入输出 feature map 的宽高。标准卷积的算法：

$G_{k,l,n} = \sum_{i,j,m}{K_{i,j,m,n} \cdot F_{k+i-1, l+j-1,m}}$

标准卷积的计算复杂度：

$D_K \cdot D_K \cdot M \cdot N \cdot D_F \cdot D_F$

其中 M 是输入通道数，N 是输出通道数， $D_K \times D_K$ 是 kernel size， $D_F \times D_F$ 是 feature map size。

而 depthwise 卷积的算法：

$\hat{G}_{k,l,m} = \sum_{i,j}{\hat{K}_{i,j,m} \cdot F_{k+i-1, l+j-1,m}}$

计算复杂度：

$D_K \cdot D_K \cdot M \cdot D_F \cdot D_F$

depthwise 卷积加上 1x1 卷积，计算复杂度：

$D_K \cdot D_K \cdot M \cdot D_F \cdot D_F + M \cdot N \cdot D_F \cdot D_F$

二者相除，这种卷积计算复杂度减少了：

$\frac{1}{N} + \frac{1}{D_K^2}$

其中，MobileNet 使用 3x3 卷积，可以提速 8～9 倍，同时对准确率影响不大。

超参数

宽度超参数 $\alpha \in (0,1]$ ，把输入输出 $M, N$ 变成 $\alpha M, \alpha N$ 。通过设置 $\alpha$ ，参数尺寸可以缩减约 $\alpha^2$ 。

分辨率超参数 $\rho \in (0,1]$ ，把 feature map $D_F \cdot D_F$ 变成 $\rho D_F \cdot \rho D_F$ 。通过设置 $\rho$ ，计算量可以缩减约 $\rho^2$ 。

MobileNetV2

引入的新的网络结构：inverted residual with linear bottleneck

与 resnet 不同，输入层先用 conv 1x1 降维，在使用 Dwise conv 3x3 + Pointwise 1x1 代替原先的标准卷积。

与 MobileNetV1 bottleneck 使用非线性函数 ReLU 不同，linear bottleneck 输出层使用线性函数 conv 1x1。原因是：理论上，ReLU 在高维空间能有效增加非线性，但在低维空间（Depthwise Conv 后）会丢失信息，参见论文附录A；实验上，导致准确率损失。

Dwise 使用 ReLU6，当低精度运算时有更好的鲁棒性。

MobileNetV2 的 Keras 实现可参考： github

SqueezeNet 17’

TODO

Optical Flow

Posted on 2018-06-16

光流法

AI 精彩视频剪辑：战术竞技类游戏直播

Posted on 2018-05-08

简介

直播平台每天都会产生海量的游戏直播视频，同时有很多内容作者从直播视频中剪辑精彩片段，进行二次创作。然而精彩视频剪辑工作，需要人工浏览视频并找出精彩片段，用视频编辑软件进行剪辑，耗费大量时间和精力。

为了解决这个问题，我们尝试用 AI 完成精彩视频剪辑的工作，并借助 TGL腾讯游戏玩家创作联盟实现视频一键多渠道（看点、企鹅号、今日头条）发布。

DEMO:

视频静态区域检测

Posted on 2018-02-26

TODO

小波变换简介

Posted on 2018-02-24

小波变换是一种变换分析方法，提供了一个随频率改变的时间-频率窗口，克服了 Fourier 变换的缺点：

小波变换比傅立叶变换能更好地处理不稳定信号。Fourier basis function 只 localize 频率，不 localize 时间。微弱的频率改变，在傅立叶变换后影响了所有时域。而 wavelets basis function localize both 频率和时间。
小波变换对很多函数，都有非常紧凑的结果，起到 sparse coding 的作用。比如 FBI 用小波变换作为指纹压缩的标准，达到 20:1 的压缩率。
快速小波变换 $O(n)$ 通常比 FFT $O(n \cdot \log_2(n))$ 速度更快。
对突变信号（比如 0-1 信号），小波变换能克服傅立叶变换的 gibbs 效应。

母小波

简单的说，母小波函数 $\psi(t)$ 必须满足以下条件：

$\begin{aligned} &\int^{\infty}_{-\infty} |\psi(t)|^2 dt = 1, i.e. \psi \in L^2(\mathbb R) \\ &\int^{\infty}_{-\infty} |\psi(t)| dt = 1, i.e. \psi \in L^1(\mathbb R) \\ &\int^{\infty}_{-\infty} \psi(t) dt = 0 \end{aligned}$

变换公式

$X(a,b)=\frac{a}{\sqrt b}\int^{\infty}_{-\infty} x(t) \Psi(\frac{t-1}{b})dt$

傅立叶变换

提出假设： $H_0$ 算法 B 与算法 A 人均付费一致

短时距傅立叶变换

$X(t,f)=\int^{\infty}_{-\infty} w(t-\tau) x(\tau)e^{-j2\pi f\tau}d\tau$

其中符号 $f$ 频率， $t$ 时间， $a$ 时间， $b$ 尺度

Haar

Haar 是最简单最原始一种小波变换。

公式

$\Psi_{jk}(x) = const \cdot \Psi(2^j x - k)$

[1] Vidakovic, Brani, and Peter Mueller. “Wavelets for kids.” Instituto de Estadística, Universidad de Duke (1994). PDF

[2] Wiki URL

[3] 知乎 URL

我的博客即将搬运同步至腾讯云+社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=3vtdjkbagyck4

CNN：目标检测

Posted on 2018-01-22

Multi-shot 方法

R-CNN

Ross Girshick et. al. 在 2014 [2] 提出 R-CNN，用于 object detection 和 sementic segmentation，比 VOC 2012 的最好模型 mAP (mean average precision) 提升了 30%；在 ILSVRC2013 mAP 达到 31.4%。

R-CNN 使用 Region Proposal 提取出 2000 个 ROI （感兴趣区域），对每个 ROI 使用 CNN + SVM 进行分类如猫、狗、背景。

r-cnn

在 ILSVRC 2012，CNN AlexNet 在图像分类取得了很好的成绩。为填补 CNN 在 object detection 的鸿沟，本文主要解决两个问题：

如何用深度网络进行 object detection

以往方法有 1. CNN Softmax + Regressor [4]，缺点精度不高 2. 粗暴的 sliding-window detctor，如 ILSVRC2013 冠军 Overfit [3]，缺点计算代价高。本文通过 category-independent region proposal 方法，在测试时，该方法生成 2k 张候选截图做为输入，用 category-specific SVM 分类。目前有多种 region proposal 方法，本文用 selective search [4]。分类后，用一些后处理方法来 refined box 以提升精度。
如何用小容量样本，训练高容量 CNN

以往方法用 unsupervised pre-train + supervised fine-tuning 训练。本文用大数据集 supervised pre-train (ILSVRC) + 小数据集 supervised fine-tuning (PASCAL)，对结果有显著提升。使用 AlexNet 的 pre-train model，把最后一层 4048 x 1000 改成 4048 x 21 (PASCAL 的类别数目)。在 CNN 的输出层，用 category-specific SVM 模型完成分类任务；category-independent linear regression 完成定位，输出 box 坐标。

SPPNet

引入 Spatial Pyramid Pooling，SPP结构从细密和粗糙级别上分割图像，然后融合局部的特征。SPP有3个优势：

任意size和scale输入，产生固定的输出特征表示，提取整个图片在不同尺度的特征
使用多级spatial pooling layer（多个尺寸的pooling），多级pooling对于物体形变具有鲁棒性
允许我们在各种size和scale下训练网络，可以增加样本个数（类似数据增益），防止过拟合

Fast R-CNN

R-CNN 存在缺点：

测试运行速度慢（50 sec），由 2k region proposal 导致
SVM 训练时无法更新 CNN 参数
复杂的 CNN fintune + SVM + Regressor 三阶段训练流程

为解决 R-CNN 这些问题，Girschick 在 ICCV 2015 [5] 提出 Faster R-CNN，改进有：

Region of Interest Pooling 机制，让 region proposal 在 conv 后执行，在高阶 feature map 做区域回归和分类，利用共享CNN计算提升测试速度
SVM 改成 softmax，训练时更新 CNN 参数
用 multi-task loss 简化训练流程，end-to-end

在 PASCAL 训练时间从 84 小时降低到 9.5 小时，测试时速度提升 146x，mAP 稍微有提升。

实际每张图片处理时间从 50 sec 到 2 sec。

其中 ROI pooling layer 结构如下图：

Fast R-CNN

ROI pooling layer 是一个max pooling layer。假设有两个超参数 $H$ 、 $W$ 把输入的 patch 划分成 $H \times W$ 个小方格，假设投影的每个 ROI 的 patch 为 $h \times w$ ，则每个小方格尺寸是 $h/H \times w/W$ 。而在每个方格中，执行 max pooling layer 操作，两层 FC 后得到 ROI 特征向量，最后分别经过一层 FC 进入 bbox regressor 和分类 softmax 。

损失函数：

$L(p,u,t^u,v)=L_{cls}(p,u) + \lambda [u \ge 1] L_{loc} (t^u, v)$

其中 $L_{cls}(p,u) = -\log p_u$ 是分类 log 损失； $L_{loc}$ 是 bbox 损失。 $u$ 是类别， $v=(v_x,v_y,v_w,v_h)$ 是真实 bbox 坐标， $t$ 是预测 bbox 坐标。 $[u \ge 1]$ 表示只计正样本的 bbox 损失。

$L_{loc}(t^u, v)=\sum_{i \in {x,y,w,h}} \text{smooth}_{L1}(t_i^u - v_i)$

Faster R-CNN

何凯明在 NIPS 2016 发表 Faster R-CNN [6]，通过降低计算瓶颈 Region Proposal 部分，提出 Region Proposal Network 提升速度，是的检测速度达到实时 0.2 sec / 张图像。

RPN 输入图片，输出一系列 bbox 和对应的 objectness score。为了复用 CNN 的计算，我们假设 RPN 和 CNN 共享卷基层。在 conv feature map 上用 $n \times n$ 的滑动窗口提取特征（256-d）加 ReLU，随后通过两个 FC 层—— cls layer 和 reg layer 输出物体分数和物体区域。在每个滑动窗口区域，都有一个anchor，对应 k 个 region proprosal（4k reg 坐标和 2k cls）。

最后，用 RPN 得到的区域，用 ROI pooling layer + softmax classifier 完成物体检测任务。

在一个网络中的四个 loss：

RPN classification (good / bad)
RPN regression (anchor -> proposal)
Fast R-CNN classification (over class)
Fast R-CNN regression (proposal -> box)

One-shot 方法

YOLO

速度可以达到 115 FPS，但是准确率不如 R-CNN。

YOLO 把 bounding box 回归和图像分类放入同一个网络。首先把图片划分成 7x7 个 grid，每个 grid 有 B 个 base box，每个 base box 输出 confidence dx dy dw dh 和 C 个类的分数，即网络输出 7 x 7 x (5 * B + C)。

优点：

简单，单一网络
快
整张图像做为输入，能对全局信息进行建模，避免 R-CNN 对背景错误分类的问题
能学习到图像的泛化表示，比如在训练时用自然图像，在测试时用艺术图像也能工作

缺点：

未达到 state-of-art 方法的进度
精度不高，无法处理大分辨率图像的小物体

模型结构：

输入图像划分为 7x7 的 grid
每个 grid 输出 B 个 bounding box 的 (dx, dy, dw, dh, confidence) ，和分类结果 C，其中 confidence 表示 $IOU\frac {truth}{pred}$

cnn-variant-yolo-fig1

损失函数定义：

$\begin{aligned} &\lambda_{coor} \sum_{i=0}^{S^2} \sum_{j=0}^B \mathbb 1_{ij}^{obj} \bigg[(x_i-\hat x_i)^2 + (y_i-\hat y_i)^2\bigg] \\ &+ \lambda_{coor} \sum_{i=0}^{S^2} \sum_{j=0}^B \mathbb 1_{ij}^{obj} \bigg[(\sqrt{w_i} - \sqrt{\hat w_i})^2 + (\sqrt{h_i} - \sqrt{\hat h_i})^2\bigg] \\ &+ \sum_{i=0}^{S^2} \sum_{j=0}^B \mathbb 1_{ij}^{obj} (C_i - \hat C_i) ^2 \\ &+ \lambda_{noobj} \sum_{i=0}^{S^2} \sum_{j=0}^B \mathbb 1_{ij}^{noobj} (C_i - \hat C_i) ^2 \\ &+ \sum_{i=0}^{S^2} \mathbb 1_{ij}^{noobj} \sum_{c \in classes} (p_i(c) - \hat p_i(c))^2 \end{aligned}$

其中用 sum-square error 因为容易优化，尽管和我们最大化 mAP 的目标不完全一致。另外，大部分 box 不包含任何类别，训练时使得包含 object 的 box confidence 趋于 0。为解决这个问题，引入 $\lambda_{coord}=5$ , $\lambda_{noobj}=0.5$ ，减少不包含 object 的 loss，增加包含 object 的 loss。

YOLOv2

RetinaNet

FAIR 在 2017 提出 focal loss，改进 SSD 结构前背景样本悬殊的问题，提升识别准确率。其中 $\gamma \gt 0$ 减少成功分类样本的损失（ $p_t \gt .5$ ），把更多注意力放在难的、错误分类问题上。

$\begin{aligned} CE(p_t) &= -\log(p_t) \\ FL(p_t) &= -(1-p_t)^\gamma \log(p_t) \\ \end{aligned}$

FL 取不同参数的训练收敛结果：

FocalLoss

论文实验的网络结构如下，另外 loss 也可用于 R-CNN 结构。

RetinaNet

其他技巧

Data augmentation，clip + flip 混合使用。

在 supervised pre-trained model 基础上 supervised fine-turning，可以在训练集样本稀少的情况下，有显著提升 [2]。

Instance Segmentation

Mask R-CNN

He et. al. 2017 提出 Mask R-CNN [8]，在 Fast R-CNN 基础上，做 instance segmantation，精确到像素，同时可以做 pose detection。

引用

[1] Lecture 11 Detection and Segmentation, Stanford University School of Engineering Video

[2] Girshick, Ross, et al. “Rich feature hierarchies for accurate object detection and semantic segmentation.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2014. PDF

[3] Sermanet, Pierre, et al. “Overfeat: Integrated recognition, localization and detection using convolutional networks.” arXiv preprint arXiv:1312.6229 (2013). PDF

[4] CS231n Lecture 8 - Localization and Detection Video

[5] Girshick, Ross. “Fast r-cnn.” Proceedings of the IEEE international conference on computer vision. 2015. PDF

[6] Ren, Shaoqing, et al. “Faster R-CNN: Towards real-time object detection with region proposal networks.” Advances in neural information processing systems. 2015. PDF

[7] YOLO Homepage YOLO900 PDF YOLO PDF

[8] He, Kaiming, et al. “Mask r-cnn.” arXiv preprint arXiv:1703.06870 (2017). PDF

[9] Lin T Y, Goyal P, Girshick R, et al. Focal loss for dense object detection[J]. IEEE transactions on pattern analysis and machine intelligence, 2018. PDF

[10] SSD: Single Shot MultiBox Detector PDF

[11] 读 Focal Loss URL

CNN：细粒度分类

Posted on 2018-01-21

Bi-CNN

bcnn

细粒度的分类问题，fine-grained image classification，如花的品种识别，十分困难。

一种解决方法称为 part-based，是定位特征区域，如花瓣，然后用 CNN 分类，这种方法的缺点是标注成本高。

另一种解决方法 feature-based，是用鲁棒的特征：VLAD，Fisher + SIFT。这种方法不依赖训练数据，但是效果不如 part-based 方法。

Lin et. al. 提出的 Bi-CNN [1]，克服以上两种方法的缺点，可以更好的解决细粒度分类问题。同时，这种结构和人类认知的 ventral stream (what pathway) & dorsal stream (where pathway) 相似。

实验中，B-CNN 效果比 FC-CNN 高出10% 左右。其中 w/ ft 表示识别 localization 后的图像。

bcnn

找出最大化激活 filter 的图片区域，发现 B-CNN 能够学习到不同部位的特征，以完成 fine-grained 图像分类任务：

bcnn

SCDA

DCGAN

Reference

[1] Lin, Tsung-Yu, Aruni RoyChowdhury, and Subhransu Maji. “Bilinear cnn models for fine-grained visual recognition.” Proceedings of the IEEE International Conference on Computer Vision. 2015. PDF

Backprop

Posted on 2018-01-18

Backprop 算法的推导

给定样本集合 $\{(x^{(1)}, y^{(1)}), \cdots, (x^{(m)}, y^{(m)})\}$ ，我们可以用批量梯度下降法来求解神经网络。对于单个样本 $\{(x, y)\}$ ，方差代价函数是

$J(W,b;x,y)=\frac{1}{2} ||h_{w,b}(x) - y||^2$

定义整体代价函数为

$\begin{aligned} J(w,b) &= \bigg[\frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)}, y^{(i)})\bigg] + \frac {\lambda} {2} \sum_{l=1}^{n_l-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}}\bigg(W_{ji}^{(l)}\bigg)^2 \\ &= \bigg[\frac{1}{m} \sum_{i=1}^m \big(\frac{1}{2} ||h_{W,b}(x^{(i)}) - y^{(i)}||^2\big)\bigg] + \frac {\lambda} {2} \sum_{l=1}^{n_l-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}}\bigg(W_{ji}^{(l)}\bigg)^2 \end{aligned}$

其中第一项是均方差项，第二项是正则（权重衰减）项（对偏置项 $b$ 导正则化作用不大，所以省略）。

梯度下降法中，每次迭代更新参数规则

$\begin{aligned} W_{ij}^{(l)} &= W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) \\ b_{i}^{(l)} &= b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_i^{(l)}} J(W,b) \end{aligned}$

其中 $J(W,b)$ 的偏导数为

$\begin{aligned} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) &= \frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b;x^{(i)}, y^{(i)}) + \lambda W_{ij}^{(l)} \\ \frac{\partial}{\partial b_{i}^{(l)}} J(W,b) &= \frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial b_{i}^{(l)}} J(W,b;x^{(i)}, y^{(i)}) \end{aligned}$

反向传播的思路：

给定样本 $(x,y)$ ，先前向传导计算出网络中所有激活值
对 $l$ 层的第一个节点 $i$ ，计算其残差 $\delta_i^{(l)}$
- 对最终输出节点，残差 $\delta_i^{(n_l)}$ 等于激活值与样本的差
$\begin{aligned} \delta_i^{n_l} &=\frac{\partial}{\partial z_i^{(n_l)}} \frac{1}{2} ||y - h_{W,b}(x)||^2 \\ &= \frac{\partial}{\partial z_i^{(n_l)}} \frac{1}{2} \sum_{j=1}^{S_{n_l}} (y_i - a_j^{(n_l)})^2 \\ &= \frac{\partial}{\partial z_i^{(n_l)}} \frac{1}{2} \sum_{j=1}^{S_{n_l}}(y_j - f(z_j^{(n_l)}))^2\\ &= -(y_i - f(z_i^{(n_l)})) f'(z_i^{(n_l)})\\ &= -(y_i - a_i^{(n_l)}) f'(z_i^{(n_l)}) \end{aligned}$
- 对隐藏节点 $(l=n_l -1, n_l - 2,\cdots,2)$ ，基于节点残差的加权平均值计算 $\delta_i^{(l)}$ ，以 $a_i^{(l)}$ 作为输入
$\delta_i^{(l)} = \bigg( \sum_{j=1}^{s_{l+1}} W_{ji}^{(l)} \delta_j^{(l+1)} \bigg) f'(z_i^{(l)})$
计算偏导数（根据链式法则，例子见 [2]）

$\begin{aligned} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b;x,y) &= a_j^{(l)} \delta_i^{(l+1)} \\ \frac{\partial}{\partial b_{ij}^{(l)}} J(W,b;x,y) &= \delta_i^{(l+1)} \end{aligned}$

用矩阵 - 向量表示法重写以上算法，用 $\cdot$ 表示向量乘积，BP 算法步骤为

进行前馈传导计算，得到 $L_2, L_3, \cdots, L_{n_l}$ 的激活值
对输出层（第 $n_l$ 层），计算

$\delta^{(l)} = - (y - a^{(n_l)}) \cdot f'(z^{(n_l)})$

对隐藏层 $l=n_l - 1, n_l - 2, n_l - 3, \cdots, 2$ 的各层，计算

$\delta^{(l)} = \big( (W^{(l)})^T \delta^{(l+1)} \big) \cdot f'(z^{(l)})$

计算偏导数值

$\begin{aligned} \nabla_{W^{(l)}} J(W,b;x,y) &= \delta^{(l+1)} (a^{(l)})^T \\ \nabla_{b^{(l)}} J(W,b;x,y) &= \delta^{(l+1)} \end{aligned}$

参考

[1] UFLDL 反向传导算法 URL

[2] Principles of training multi-layer neural network using backpropagation URL

CNN 可视化解释：Saliency Maps

Posted on 2018-01-12

Image-Specific Class Saliency Visualization

给定一个图像和 CNN 的分类结果，图像中哪个像素对分类结果贡献大？

Simonyan et. al. 在文章 [1] 提出 saliency maps 解决这个问题。

saliency-map-fig-1

给定图像 $I^{m \times n}$ ，求 salency map $M^{m \times n}$

记把输入 $I$ 在 ConvNet 的对应 c 类的输出分数为（其中 $I$ 被一维化）

$S_c(I)$

将在 $I_0$ 处其一阶泰勒展开，得到等式

$S_c(I) \approx w^T I + b$

其中 $w$ 是 $S_c$ 在 $I_0$ 的一阶导数，用 single backprop 方法求解

$w=\frac{\delta S_c(I)}{\delta I} \bigg|_{I_0}$

计算 saliency map $M$

$M_{ij}=\max_{channel} |w_{(i,j,channel)}|$

其中，用一阶导数表示 saliency map 的另外一种解释，是数值越大表明对结果影响越大，颜色越深。

另外，用 saliency map 的结果，可以辅助 GraphCut.

Class Model Visualisation

给定一个模型，如何将其可视化？Simonyan et. al. 在文章 [1] 提出 class representiative image generation 方法：

以 $S_c$ 表示 ConvNet 对类别 C 的评分函数（softmax 的输入），设最优化目标

$\arg \max_I S_c(I) - \lambda ||I||^2_2$

初始化

$I_0 = \frac{1}{n} \sum_{i=1}^n I_i$

通过 backprop 梯度下降求解 $I$ ，得到每类的图像

saliency-map-fig-0

Deconv Reconstruction

[1] 的作者与 Deconv Reconstruction 方法 [2] 进行了对比，详见 [1] PPT

saliency-map-fig-2

[1] Simonyan, Karen, Andrea Vedaldi, and Andrew Zisserman. “Deep inside convolutional networks: Visualising image classification models and saliency maps.” arXiv preprint arXiv:1312.6034 (2013). APA PDF PPT

[2] Zeiler, Matthew D., and Rob Fergus. “Visualizing and understanding convolutional networks.” European conference on computer vision. Springer, Cham, 2014. APA

ResNet 学习笔记

Posted on 2018-01-02

MSRA 的 Kaiming He et. al. 在 CVPR15 发表了 ResNet ^[1]，即残差网络，在网络的输入层加入了残差函数，使得更深层神经网络优化更容易。用 152 层 ResNet （比 VGG 深 8 倍）学习 ImageNet 数据集，达到 3.57% 的错误率在 ILSVRC 2015 中名列第一。

在 Deep CNN 中，通常可以增加网络层数，来加强学习能力。

随着网络加深，通常会遇到两个问题：

梯度消失 / 梯度爆炸，通常可以用 Batch Norm / 梯度截断方法解决
退化问题：train accuracy 趋于饱和，这不是过拟合引起的，因为增加层数，train error 会随之增加，如 Figure 1 所示。它意味着不是所有的神经网络都容易优化。

对退化问题，有一个解决方法：构建更深的模型时，added layer 是恒等映射，其他 layers 是从学习好的浅层模型复制过来。这种解决方法表明，更深的模型，相对于浅层的模型，不应该产生更高的训练误差。实验显示，目前 solver 无法很好地求解。

fig1

在这篇论文中，提出了 deep residual learning framework 来解决这个退化问题。让每个 layer 拟合残差映射（residual mapping），而不是拟合 underlying mapping，如 Figure 2 所示。

fig1

如果 add 操作输入和输出的大小不同，那就可以使用零填充或投射（通过 1×1 卷积）来得到匹配的大小。

记原始映射（original mapping）为 $\mathcal F(\mathbf x) := \mathcal H(\mathbf x) - \mathbf x$ ，残差映射（residual mapping）为 $\mathcal H(\mathbf x)$ 。我们假设残差映射更容易优化。极限情况下，如果恒等映射（identity mapping）是最优的，那么把 residual push to zero 比拟合恒等映射（stack of nonlinear layers）更容易。

ResNet 作者将这些问题归结成了一个单一的假设：直接映射是难以学习的。而且他们提出了一种修正方法：不再学习从 $x$ 到 $H(x)$ 的基本映射关系，而是学习这两者之间的差异，也就是「残差（residual）」。然后，为了计算 $H(x)$ ，我们只需要将这个残差加到输入上即可。

其中为 identity $\mathbf x$ 是 shortcut connection，它不增加模型的计算复杂度和参数，同时也容易用现有框架（Keras / Caffe）实现。

论文的实验表明：

Deep ResNet 容易优化，而 CNN 随着深度增加，train error 增加
ResNet 比 CNN 更容易通过增加深度（500~1k 层）来提高准确率，参数更少，训练时间更快。

网络结构如 Figure 3 所示：

fig1

在 keras.applications.resnet50 中 ResNet 结构定义如下。其中 conv_block 和 identity_block 的区别是 identity $\mathbf x$ 增加了卷积计算。

x = Conv2D(64, (7, 7), strides=(2, 2), padding='same', name='conv1')(img_input)
x = BatchNormalization(axis=3, name='bn_conv1')(x)
x = Activation('relu')(x)
x = MaxPooling2D((3, 3), strides=(2, 2))(x)

x = conv_block(x, 3, [64, 64, 256], stage=2, block='a', strides=(1, 1))
x = identity_block(x, 3, [64, 64, 256], stage=2, block='b')
x = identity_block(x, 3, [64, 64, 256], stage=2, block='c')

x = conv_block(x, 3, [128, 128, 512], stage=3, block='a')
x = identity_block(x, 3, [128, 128, 512], stage=3, block='b')
x = identity_block(x, 3, [128, 128, 512], stage=3, block='c')
x = identity_block(x, 3, [128, 128, 512], stage=3, block='d')

x = conv_block(x, 3, [256, 256, 1024], stage=4, block='a', strides=(2, 2))
x = identity_block(x, 3, [256, 256, 1024], stage=4, block='b')
x = identity_block(x, 3, [256, 256, 1024], stage=4, block='c')
x = identity_block(x, 3, [256, 256, 1024], stage=4, block='d')
x = identity_block(x, 3, [256, 256, 1024], stage=4, block='e')
x = identity_block(x, 3, [256, 256, 1024], stage=4, block='f')

x = conv_block(x, 3, [512, 512, 2048], stage=5, block='a', strides=(2, 2))
x = identity_block(x, 3, [512, 512, 2048], stage=5, block='b')
x = identity_block(x, 3, [512, 512, 2048], stage=5, block='c')

# x = AveragePooling2D((7, 7), name='avg_pool')(x)
x = AveragePooling2D((1, 1), name='avg_pool')(x)

x = Flatten()(x)
x = Dense(n_labels, activation='softmax', name='fc')(x)

1x1 卷积

下图是一个更深的残差函数，称为 Bottleneck，使用了 1x1 卷积对输入输出进行降维，加速计算，减少网络参数：

其中 1x1 卷积的作用，是在保持 feature map 尺度不变的前提下，线性组合不同channel的像素点，增加或减少 depth，完成升维或者降维。

经过激励层，1x1 卷积在前一层学习表示上添加了非线性激励，提升网络表达能力。

He, Kaiming, et al. “Deep residual learning for image recognition.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. PDF ↩︎

生成模型

Posted on 2017-10-15

PixelRNN / Pixel CNN

Variational Autoencoders

GAN

Ian. Goodfellow NIPS2014[1]，为了学习 generator 在数据 $x$ 上的分布 $p_g$ ，定义输入噪声变量 $p_z(z)$ ，定义从 $z$ 到数据空间的映射函数 $G(z;\theta_g)$ ，其中 $G$ 是由可微分的、multilayer perception 组成的函数。定义 MLP 组成的判别函数 $D(x;\theta_d)$ ，输出 0～1 表示 $x$ 来自于真实数据还是 $p(z)$ 的概率。

损失函数表示为

$\min_G \max_D V(D,G) =\mathbb E_{x\sim p_{data}} [\log D(x) + \mathbb E_{x \sim p_z(z)} [\log (1 - D(G(z)))]$

判别函数 $D$ 希望避免被欺骗，即最大化目标函数，使得 $D(x)$ 接近 1 而 $D(G(z))$ 接近 0。

生成函数 $G$ 希望以假乱真，即最小化目标函数，使得 $D(G(z))$ 接近 1。

GAN w/ Conv

Ian Goodfellow, ICLR 2016

CycleGAN

Zhut et al. 2017

Ref

[1] Generative Adversarial Networks, Goodfellow et al., NIPS 2014, PDF

[2] Unsupervised representation learning with deep convolutional generative adversarial networks, Goodfellow et al., ICLR 2016, PDF

Lecture 13 Generative Models, Serena Yeung, Stanford YouTube

MinMax, Strategies of Play, Game Thery, Dan Vekhter et al., Stanford HTML

无约束最优化问题求解

Posted on 2017-08-29

无约束最优化问题求解方法的学习笔记

iOS 私有 API 调用检测机制探讨

Posted on 2017-08-23

最近发现部分 App 以字符串拼接的方法调用私有 API，在提交 AppStore 审核后被发现打回修改的案例。

对于开发者提交的二进制文件，Apple 是如何检查出私有 API 的调用？本文尝试探讨可能的检测机制，以及每种机制的漏洞。

在线学习方法概述

Posted on 2017-08-21

推荐系统算法常常用到逻辑回归算法，而传统的批量学习算法如 SGD 无法应对大规模、高维的数据集和实时数据流。为了解决这个问题，在线最优化算法如 TG [1]、FOBOS [2]、RDA [3]、FTRL [4,5,6] 应运而生，下面将介绍、对比这些算法。

TODO

GloVe

Posted on 2017-08-18

介绍一种 word embedding 方法。

GBDT

Posted on 2017-08-17

GBDT（Gradient Boosting Descision Tree）, 梯度提升决策树, 又名 MART（Multiple Additive Regression Tree）, 是由多颗回归决策树组成的 Boosting 算法, 常用于 CTR 预估. 本文介绍了决策树、Boosting 决策树、Gradient Boosting 决策树的算法原理和实现.

Reinforce Learning

Posted on 2017-08-11

强化学习笔记。

Deep Learning

Posted on 2017-08-11

深度学习笔记

Activation

Posted on 2017-08-11

对比、介绍神经元的激活函数。

Factorization Machine

Posted on 2017-08-08

对 LR 最朴素的特征组合就是二阶笛卡尔乘机，但是特征组合存在如下问题：

两两组合导致特征维度灾难
组合后的特征不见得都有效，事实上大部分可能无效
组合后的特征样本非常稀疏，意思就是组合容易，但是并不能在样本中找到对应的组合出现，也就没有办法在训练时更新参数。

Factorization Machine [1] 应运而生，优点有：

适用于稀疏数据
FM (2-way) 比 LR 多了二阶 kernel，适用于大数据，线性复杂度，可以用 primal objective 而不是 dual objective 优化（如 SVM）
通用的预测模型，适用于任何实数特征。

下面是 [1] 的学习笔记。

Matrix Factorization

Posted on 2017-08-07

Matrix Factorization 是一种协同过滤思想的方法，用于物品推荐和评分预测。

YAHOO 团队在 Netflix Prize 应用 Matrix Factorization 并取得较好的成绩，效果远超传统协同过滤方法 [1]，我们在下文详细展开介绍。

尝试改进微信读书个性化推荐：一个基于 CTR 预估的方法

Posted on 2017-07-07 | In Dev

引言

微信读书的书籍个性化推荐包括：

冷启动用户的书籍推荐，如发现 tab – 新手卡片，为新注册用户推荐书籍，方法参见文章微信读书冷启动用户书籍推荐初探：一个借助微信用户画像的方法微信读书冷启动推荐实战：一种基于用户属性的方法
。
基于协同过滤（Item-CF / Word2vec）的书籍推荐，如于书城 – 搜索 – 猜你喜欢，为老用户推荐书籍。

为提升 2 的效果，本文设计了一个离线实验，用 CTR 预估方法做书籍个性化推荐，发现效果（准确率、召回率）较现网方法（Word2vec）提升接近一倍。

iOS App 启动必 crash 监控

Posted on 2017-07-07 | In Dev

摘要

在 iOS 11 Beta 刚刚发布时，有用户在微博反馈：升级到 iOS 11 Beta 后，微信读书 App 遇到启动必 crash 的绝境，无法使用。

feed_back

用户看到的界面，是我们开源的 iOS 启动连续闪退保护方案提示。

调试发现，是一段 iOS 11 不兼容的代码引发的问题。我们通过修改不兼容代码，解决了问题。

等到现网用户反馈，为时太晚，如何把启动必 crash 问题纳入监控？

我们设计了一个特征值以判断这个问题，并扩展了 iOS 启动连续闪退保护方案，提供了日志上报接口，帮助开发者在第一时间发现启动必 crash 问题。

R 语言线性回归应用：拟合 iOS 录音波形图

Posted on 2017-04-28

引言

微信读书有一个录音功能需求：

录音时绘制音频波形，音频以 wav 格式保存
再次进入界面，加载 wav，重新渲染音频波形

步骤 1 通过 NSRecorder.averagePowerForChannel 方法获取当前录音的分贝 $L_p$ 数组，绘制波形图

lecture_track_lm

步骤 2 需要从 wav 推算出分贝波形图。然而根据分贝公式推算出来的结果如下图所示，与步骤 1 不一致：

lecture_track_lm

不一致的原因，可能是步骤 1 通过硬件 DSP 计算得到 mic 的分贝，与 2 通过公式计算 wav 分贝的算法不同。

我们要解决这样的问题：拟合一个公式，输入一段 wav 采样的均方根值 $p_{rms}$ ，输出估算的分贝 $\tilde{L_p}$ ，使其近似等于 averagePowerForChannel 返回的值 $L_p$ 。

我们通过收集数据，建立线性回归模型，调参，验证等步骤，成功得到了波形图还原方程：

$\tilde{L_p} = -80 + 6 \log_{2} {p_{rms}}\ dB$

最终，还原了近似波形图：

lecture_track_lm

HTML

Posted on 2017-03-21

机器学习笔记

基于word2vec协同过滤推荐

Posted on 2017-03-06 | In Algorithm

引言

在文章学习协同过滤推荐 \w 100行Python代码中，介绍了基于物品的协同过滤推荐，根据 user-item 评分矩阵，找出与给定 item 评分最接近的物品，作为推荐结果。

在本文中，把书籍名称看作单词，以用户喜欢的书籍看作句子，利用 word2vec 模型构建了一个书籍的向量空间。对给定书籍，找出与其距离最近的书籍，作为推荐结果。

本文用 Python 60 行代码实现了一个 Demo，得到每本书籍在向量空间的表示，输出基于书籍的协同过滤推荐结果。

微信读书冷启动推荐实战：一种基于用户属性的方法

Posted on 2016-12-14 | In Algorithm

引言

在文章《微信读书冷启动书籍推荐初探：一个借助微信用户画像的方法
》1，我们发现用户的阅读偏好与用户属性（性别、年龄、n 线城市、公众号阅读偏好）相关。基于这个发现，我们利用用户属性，给冷启动的新注册用户做个性化推荐，效果较编辑推荐提升约 50%。

说明图片

学习协同过滤推荐 \w 100行Python代码

Posted on 2016-12-09 | In Dev

引言

用一百行 Python 代码，入门协同过滤推荐。

thai-photos

Posted on 2016-10-23 | In Life

初学潜水

Posted on 2016-10-15 | In Life

在 2016 国庆节假期，从广州前往泰国涛岛 Koh Tao 学习潜水，尝试考取入门级别的开放水域（Open Water）潜水员证书。

微信读书冷启动用户书籍推荐初探：一个借助微信用户画像的方法

Posted on 2016-10-15 | In Algorithm

引言

微信读书 App 中的书籍推荐系统，逐渐开始在运营活动中（每周热榜、新手卡片）使用，尝试从技术侧帮助运营侧提高转活动的化率。

对微信读书的活跃用户，我们根据其读书时长、点评书等用户行为，做书籍推荐。对微信读书新增用户，由于缺少用户行为数据，无法使用这种方法做推荐，此类问题常被称为推荐系统冷启动问题。

然而，我们发现微信用户画像，比如基础属性（年龄、城市、性别等）和公众号阅读兴趣等，与微信读书用户的阅读兴趣相关。借助微信用户画像进行书籍推荐，准确率较随机推荐提升约 1 倍。

iOS 启动连续闪退保护方案

Posted on 2016-05-20 | In Dev

引言

“如果某个实体表现出以下任何一种特性，它就具备自主性：自我修复、自我保护、自我维护、对目标的自我控制、自我改进。” —— 凯文·凯利

iOS App 有时可能遇到启动必 crash 的绝境：每次打开 App 都闪退，无法正常使用App。

为了尝试解决这个问题，微信读书开发了 iOS 连续闪退保护工具：GYBootingProtection，检测连续闪退，在连续闪退出现时，尝试自修复 App：

本文探讨了连续闪退问题的产生原因、检测、修复机制，以及如何在你的项目中引入、测试和使用 GYBootingProtection。

微信读书排版引擎自动化测试

Posted on 2016-05-20 | In Dev

引言

在微信读书 App ^[1] 中，排版引擎负责把书源文件解析、渲染至屏幕，是最常用、最复杂的组件之一。而开发同学对排版引擎的日常修改，可能影响了海量书籍的排版结果。对排版引擎修改的测试耗时多、难度大、容易漏测。本文介绍了为解决测试的难题，如何逐步将人工测试步骤自动化，最终构建了一套微信读书排版引擎自动化测试流程，以确保微信读书排版引擎的质量。

尝试解决 Xcode7.1 覆盖率测试 GCDA 文件损坏问题

Posted on 2015-12-05

在升级到 Xcode7 后，项目遇到覆盖率测试输出的 GCDA 文件损坏问题。

notes-on-7-concurrency-model-in-7-weeks

Posted on 2015-06-30 | In Dev

Week 1 线程和锁

优点

易于实现，适用场景广，接近“硬件本质”。

缺点

不够抽象，难以单元测试、Debug、不可重现故障。

learn-haskell

Posted on 2015-06-16 | In Dev

—— Notes on CH8 Haskell, Seven Languages in Seven Weeks by Bruce A. Tate

引言

Haskell不同于Scala，是一门纯函数式语言，它强制使用者使用函数式语法而没有妥协。

是一门强类型定义的静态类型语言。它的**类型模型基于推断理论（in-ferred）**并被公认为是函数语言中最高效的类型系统之一。你会发现该类型系统支持多态语义并有助于人们作出十分整洁清晰的设计。
支持Erlang风格的模式匹配（pattern matching）和哨兵表达式。你也能在Haskell中发现Clojure风格的惰性求值（lazyevaluation）以及与Clojure和Erlang相同的列表推导语法。
无副作用，通过monad概念保存状态：一个Haskell函数可以返回一个有副作用并且会被延迟执行的结果.

五毛和阴谋论

Posted on 2015-05-30 | In Opinion

看了环球日报，司马南，五月网，乌有之乡，民兵智库上的文章，总有一股气，不得不吐。

这些媒体上总是有一种论调：

美国由少数人操纵，想反对中国，想竭制中国。美帝是坏人，号召国民要起来反对，打倒美国佬。美帝控制的国内媒体，宣扬西方价值观念，而对广大爱国民众、学者和言论观点则进行压制和屏蔽^[1]。

而《货币战争》上提出，美国有个罗斯柴尔德家族控制了央行，打压中国的货币体系。其中太多谬误，在知乎^[2]有详细讨论，其中有：

书中认为应当藏金于民，鼓励大家购买黄金增值保值。但在金融上对黄金是有定论的：黄金作为大宗商品，是优秀的避险工具，并且黄金价格与美元指数存在负相关。
「乱世买黄金」，预期美国经济下滑，美元疲软时，买入黄金规避风险。不是什么时候都要买的，反例正是在美国经济正在复苏的时候买黄金赔进去的中国大妈。

这些媒体把美国看做一个意志独立的，由少数财团操纵，只为自己利益着想，想打谁打谁的坏人。

似乎是一种阴谋论，而阴谋论有着不可证伪的特点：

阴谋论往往缺乏证据，荒谬的逻辑，不符合奥卡姆剃刀原则，是很多谣传的基础。但是被指责为阴谋当事人的一方，也很难证伪阴谋论的说法，许多阴谋论有不可证伪的特点，即通常说的“难以自证清白”。逻辑上，任何一件自然发生的事件，事后都可以被描绘成事先策划的。因此，说一个理论是阴谋论同时有该理论不被广为接受的意味。^[3]

这些美国想竭制中国的阴谋论观点，是建立在这样的前提下：美国是一个意志精神利益关系统一独立的个体，中美互相独立，没有利益交互。

这样的前提，把美国山姆大叔描绘得栩栩如生，能很容易被广大中国青年接受，进而转化成愤青，关注中美矛盾，而不是关注国内的矛盾。从而达到阴谋论提出者的目的——转移矛盾。咦，听起来，好像多年前抵制日货、法西斯的年代，民粹主义有些相似？

然而，事情似乎远不像两个人打架这么简单：

美国不是一个个体，它是多方利益关系的人的集合，包括美国华人，犹太人，一二代移民，商人，工人，非法移民，各个党派等等。
中国也不是一个个体。
而中、美之间，不可能是简单的对立关系。中间有复杂的利益关系交错，不是两个独立敌对的个体。比如说某领导的女儿在美国上大学，官员在美国有资产，中美公司护持股份，互有固定资产投资，中美股民互持对方股市的股票。随着市场全球化，中美之间的关系不像朝美关系那样的单纯。

如果真要打仗，天朝屁民该怎么办？

抵制美国货？挑便宜的买。

买黄金？黄金和美元走势负相关^[4]。

如果你认为中美打仗，美国尤其是美国军火商会占便宜，那么请买军火商的股票。——洛克希德—马丁公司在9.11后疯长不少。

有了市场全球化，大家都可以发战争财了。

萨达姆以欧元结算石油，招来战争

这是类《货币战争》风格的言论，类似的还有传言中国将以人民币作为出口石油结算货币，如果是真的将产生什么影响？

下面，以朝鲜为背景，探讨一下这个问题。

假设朝鲜货币（￥）兑换外币是必须经过中央银行，汇率不浮动、由央行制订。朝鲜元兑美元，6￥兑1$。

如果朝鲜要求以朝鲜币结算石油，且它的石油价格（换算成美元$）和其他国家一样，会带来怎样的结果呢？

美国家向朝鲜买石油，去朝鲜央行将美元兑换成朝鲜币，购回一桶石油（10兑60￥）。朝鲜央行收10，支出60￥。

同时朝鲜石油工人工作一个月，产出一桶石油，收入3000￥。而美国石油工人一个月收入1000$（约6000￥）。

消费物价一样（1$在美国和6￥在朝鲜都能买1袋面粉），作为一个朝鲜石油工的收入比美国石油工收入低一半。

如果，朝鲜政府宣布，朝鲜元￥继续升值，7￥兑1$。然而国内的石油价格、物价依然一样。美国用更少的$兑换一桶石油，石油出口增多，朝鲜公司进口成本降低、赚钱多了，央行的美元储备增加。有钱民众发现￥升值了，出国血拼，购置美国房产。低收入者发现钱不够出国旅游，物价无差别，生活继续。有通胀危险，物价提升，低收入者生活质量下降。（对内贬值，对外升值）
如果，朝鲜政府宣布，朝鲜元￥贬值，5￥兑1$。然而国内的石油价格、物价依然一样。美国发现要用更多的$兑换一桶石油。石油出口减少，朝鲜公司进口成本增加、赚钱少了，央行的美元储备减少。有钱民众发现￥贬值了，进口商品涨价了；低收入者的物价无差别，生活继续。有通缩危险。有通缩危险，物价下降，低收入者生活质量提高。（对内升值，对外贬值）

同时，由于是朝鲜政府、央行控制汇率，有可能高于或者低于市场价格，导致部分人在黑市炒卖货币获利，同时导致通胀或者通缩。

由此可见，前一种情况对政府、出口商、高收入人群而言是较理想的，对低收入群众而言则不利。反之亦然。

但是如果是自由浮动汇率制度，则没有上述问题。资本在跨国结算时会自己寻找最优的方案进行结算。

SCIP学习笔记

Posted on 2015-05-28 | In Dev

引言

SCIP(Structure and Interpretation of Computer Programs)^[1]是MIT自1984年起的编程入门教程，尽管最近他们用Python的课程取代了Lisp语言，但是随着工业界越来越多的应用函数编程语言，如Clojure、Scala、Racket，以及软件开发使用并发的趋势(见文章^[2]），重读SCIP是很有意义的。

SCIP分五章：构造过程抽象，构造数据抽象，模块化、对象和状态（涉及并发），源语言抽象，寄存器机器里的计算（编译器如何工作）

通过Swift学函数式编程

Posted on 2015-05-11 | In Dev

在文章SWIFT IS A LOT LIKE SCALA ^[1] 提到Swift和Scala有很大的相似之处，在某些特性甚至比Scala对函数式编程的支持更友好。笔者遂从Swift语言出发，学习函数式编程^[2] ^[3]，并记录笔记如下。

笔记：软件开发的转折——并发化

Posted on 2015-05-11 | In Dev

——文章The Free Lunch Is Over: A Fundamental Turn Toward Concurrency in Software By Herb Sutter的读书笔记

我的马克思主义观是如何崩塌的

Posted on 2015-04-19 | In Opinion

在最近一年，看了一些与社会、经济、政府有关的书，使我的先前接受（被洗脑）的马克思政治经济学观点，被彻底颠覆了。

《国富论》

《黑客与画家》

《市场的逻辑》张维迎

《从0到1》

《失控》

《社会契约论》

Google Chrome Canary：一个可以慢速调试css动画的浏览器

Posted on 2015-03-04 | In Dev

慢速调试CSS动画？以前要通过插件完成，现在集成到Chrome Canary浏览器里了，尽管它还是开发者预览版，但是这个功能是原生的哦。

有了它，就可以通过0.1~1x的速度，慢速渲染css动画，大大方便了前端开发者。

使用方法：安装Chrome Canary （需用梯子下载），打开一个带有CSS动画效果的网页，在页面空白处右键—『审查元素』，拖动Styles—Animations的控制条，即可把CSS动画速度变慢。

Chrome Canary Animation Debug Screen Shot

TODO

Posted on 2014-10-23 | In Life

研究生阶段已过一半，也找工作也告一段落。下面把学生最后阶段要完成的事情列出来，以便安排计划和督促自己。

工程：

函数式编程语言 Haswell / Erlang / Swift

Python Web

NoSQL

深入SQL

毕业设计

学术：

掌握经典的机器学习算法推导

统计概率

深度学习–图片分类，以及其他任务与传统方法做对比

3 Kaggle Problem @ ranking 30%

公开课：

完成Coursera Enroll的课程视频和课后练习：

Game Theory

每晚睡4.5小时，保持精力充沛的秘诀

Posted on 2014-08-10 | In Life

读到这篇文章：THE POWER OF THE SLEEP CYCLE，作者提到每天晚上只睡4.5小时或者3小时，白天也能精力充沛。而且达芬奇，Thomas Jefferson，建筑师福乐，爱迪生，马英九也掌握了这种技巧，而且健康并没有因此受影响：福乐和达芬奇都2倍长寿于当时的平均水平。

到底是什么秘密呢？

编程珠玑II C12笔记: rand num generator

Posted on 2014-08-10 | In Algorithm

Problem:

given m<n, generate random numbers of m within range(0..n).

问题

建模

推导

模型定义

损失函数推导

评估

参考

附录

正态分布

对数正态分布

中心极限定理

LogNormal Loss 推导

MSE Loss 推导

MAE Loss 推导

Huber Loss

对比

独热编码语言模型

矩阵分解语言模型

基于SVD

统计语言模型

N-gram

浅层神经网络语言模型

NNLM

Wordvec

SkipGram

自回归语言模型

Seq2Seq

ConvS2S

Transformer

ELMo

GPT

自编码语言模型

BERT

MT-BERT

RoBERTa

ALBERT

排列语言模型

XLNet

最新进展

MT-DNN

T5

附录

最近发表

Importance Sampling

Inverse Propensity Weighting

Delayed Bandits

GCN

Transductive / Inductive Task

GraphSage

Spatial Domain

Spectral Domain

GCN

GraphSAGE

PinSage

EGES

GraphTR

GAT

频率派

假设

参数估计

套路

举例

贝叶斯派

假设

参数估计

套路

区别

例子

参考

RNN

N vs N

N vs 1

1 vs N

N vs M / Encoder-decoder / Seq2seq(变长)

LSTM

GRU

RNN + Attention (Encoder-decoder)

Attention QKV

Self-attention

Traditional Attention